| E | xh= |
|
xi yjP | (HiGj)= |
|
xi yjP (Hi)P | (Gj)= |
|
xi P | (Hi) |
|
yjP (Gj)=E xE h. |



| E | xh= |
|
xi yjP | (HiGj)= |
|
xi yjP (Hi)P | (Gj)= |
|
xi P | (Hi) |
|
yjP (Gj)=E xE h. |
| F(q |
|
)=a. |
| D | x = | у х (x-E x)2 f(x) dx, D |
x = |
|
(xi-E x )2 pi. (5.1) |
 |
|
|||||||||||||
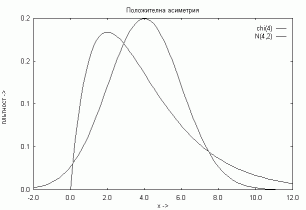
| Фигура 5.2: Положителна асиметрия | ||||||||||||||
 |
|
|||||||||||||
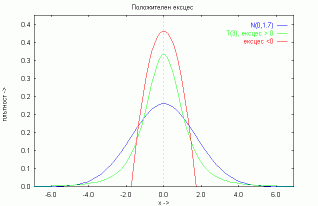
| Фигура 5.3: Положителен ексцес | ||||||||||||||
| D x і 0; | (5.6) | |||
| D x = 0 | Ы | P (x = const)=0; | (5.7) | |
| D x= | E x2 - (E x)2; | (5.8) | ||
| D ax=a2D x; | D (x+c)=Dx | |||
| D (x+h)=Dx + Dh, | ако | x^h. |

| E |x|r= E | |x|rI |
|
+ E | |x|rI |
|
і er E | I |
|
=
er P (|x| > e).
 |
| L |
|
М LrМ LpМ L1М M, 1<p<r<Ґ. |
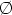 ,W}, то E e= I, E n= E .
Условното м.о. на всяка сл.в. x при условие крайното разделяне
g е проста сл.в. с константни стойности върху елементите
му. Условните м.о. удовлетворяват всички свойства на ортогоналните
проектори в Хилбертово пространство. Ако g^d, то
E g и E d комутират.
,W}, то E e= I, E n= E .
Условното м.о. на всяка сл.в. x при условие крайното разделяне
g е проста сл.в. с константни стойности върху елементите
му. Условните м.о. удовлетворяват всички свойства на ортогоналните
проектори в Хилбертово пространство. Ако g^d, то
E g и E d комутират.


