


Тема 4 Случайни величини
В тази лекция си поставяме следните цели:
-
да определим случайна величина (сл.в.);
- да определим разпределение на сл.в.;
- да дадем примери за сл.в..
Случайните събития представляват най-простия пример за
модел на наблюдение със случаен (неопределен отнапред) изход.
Често се налага да на практика наблюденията да бъдат всъщност
измервания -- резултатът от експеримента да се записва с число.
Модел на такива експерименти са случайните величини.
4.1 Прости случайни величини
Сл.в. са числови функции определени върху множеството
от елементарни събития W, като точното определение зависи
от това кои са случайните събития в W.
Определение 4.1
Нека е зададена пълната група събития (разделянето)
(H1, H2, ..., Hn). Ще казваме, че е определена проста
сл.в., ако x(w) = xi, " wО Hi, i=1,2, ..., n.
Пример 4.1
Нека разгледаме вероятностното пространство от
пример 3.2: 'Хвърляне на два зара.'
То се състои от 36 равновероятни елементарни събития. Да ги
означим
с wi,j, i,j=1,2,...,6). Да определим на това вероятностно
пространство 2 сл.в. x(wi,j)=i, h(wi,j)=j.
Намерете пълните групи на двете сл.в.
Теорема 4.1
Линейна комбинация, произведение, минимум, максимум и функция
на прости сл.в. е проста сл.в.
Доказателство: Нека пълната група събития
(H1,H2,...,Hn) съответствува на сл.в. x,
пълната група събития (G1,G2,...,Gm) на сл.в. h,
а техните стойности са съответно {x1,x2,... xn} и
{y1,y2,... ym}.
Първо ще докажем, че събитията {HiGj,
i=1, 2, ..., n, j=1,2, ..., m } образуват пълна
група.
HiGjЗ HkGl= HiHkЗ GjGl = 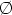 ,
когато i№ k или j№ l.
,
когато i№ k или j№ l.
|
|
HiЗ Gj=
|
|
HiЗ |
|
Gj=
|
|
HiW = |
|
Hi = W. |
Тогава сл.в. ax+bh,
x h, min(x,h), max(x,h)
ще приемат стойности, съответно, a xi+b yj,
xi yj, min(xi,yj), max(xi,yj)
за всяко елементарно събитие от събитието HiGj от
пълната група от събития.
Функцията f(x,h), съответно,
ще приема стойности f(xi,yi) върху същото събитие.

Определение 4.2
Казваме, че простите сл.в. x и h са независими, ако
е независимо всяко от събитията на едната пълна група с всяко
от събитията на другата пълна група. Бележим това с
x^h.
Покажете, че в примера с двата зара сл.в. x^h.
Определение 4.3
Ще казваме, че функцията x(.), определена на W с
стойности в R, е сл.в., ако
Lx(x)={w: x(w) < x}О A, " xО
R1.
От това определение в частност следва, че множествата
La,b(x)={w:aЈ x(w) < b}О A, "
a,bО R1. Наистина, La,b(x)=La(xi)З Lb(x).
Теорема 4.2
Всяка сл.в. може да се представи като граница на редица от
прости сл.в.
Доказателство: Нека x е ограничена сл.в., т.е. с
множество от стойности: -C Ј x(w) <C. За всяко n
можем да определим крайно разделяне на пространството:
Hi={ ai-1 Ј x(w) <ai}, където числата
ai=-C+ i*2C/n. Лесно се проверява, че множествата
Hi образуват разделяне:
HiО A,
HiЗ Hj=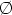 ,
И Hi=W.
Да определим простата сл.в.
xn(w)=ai, wО Hi . Тогава
|x(w)-xn(w)|Ј2C/n.
Значи x(w)= lim xn(w).
,
И Hi=W.
Да определим простата сл.в.
xn(w)=ai, wО Hi . Тогава
|x(w)-xn(w)|Ј2C/n.
Значи x(w)= lim xn(w).
Сега ще покажем, че всяка сл.в. може да се
представи като граница на редица от ограничени сл.в.
xn . Да означим
| xn(w)= |
м
н
о |
| x(w), |
L-n,n = {w:-nЈ x(w) <n} |
| 0, |
{x(w)<-n}И { nЈ x(w)} |
|
|

Теорема 4.3
Линейна комбинация, произведение и измерима функция на сл.в. е
сл.в.
Доказателството на тази теорема изисква известна математическа подготовка
и ще бъде дадено в последната секция.
4.2 Функция на разпределение и плътност
Определение 4.4
Ще наричаме функция на разпределение на сл.в. x
функцията F(x)=P (w:x(w) < x).
Функцията F(x) е монотонно ненамаляваща и непрекъсната от
ляво. Освен това F(-Ґ)=0, F(Ґ)=1.
В термини на разпределението си сл.в. се класифицират лесно.
Определение 4.5
Случайната величина, която приема стойности x1,x2,
x3,... с вероятности съответно p1,p2,p3,... се
нарича дискретна.
Естествено S pi = 1 и pi і 0. Тогава функцията
на разпределение има само скокове в точките xi, навсякъде
другаде е константа. В точката xi скокът и е равен точно на
числото pi.
Определение 4.6
Ако съществува функция f(x)і 0 такава, че
за всяко x т-Ґx f(x) dx=F(x),
ще наричаме сл.в. непрекъсната, a функцията f(x) наричаме плътност.
Тогава, разбира се F(x) е непрекъсната, т.е. няма никакви
скокове, и плътността е производна на
функцията на разпределение f(x)=F'(x) за почти всяко x.
Тук почти всяко означава всяко с изключение на изброимо много.
Естествено е, че за да бъде една функция плътност на
случайна величина, тя трябва да отговаря на две изисквания:
-
неотрицателност f(x) і 0 и
- нормираност - т-ҐҐ f(x) dx=1.
.
4.3 *Разпределения на сл.в и вектори
Да означим с 2B множеството от всички подмножества на
множеството B.
Теорема 4.4
Ако f(· ): A ѕ® B , то съответствието
''пълен праобраз'' f-1(· ): 2B ѕ® 2A
прехвърля всяка s-алгебра на B в s-алгебра на
A.
Доказателство: Само проверяваме аксиомите на s-алгебра.
Напомняме, че
s-алгебрата на Бореловите множества в Rn е минималната
s-алгебра, съдържаща всички крайни интервали: Зi {
aiЈ xi < bi), i=1,2,...,n . Нека я означим с
B. Елементите и ще наричаме Борелови множества.
Нека x е сл.в. Тогава очевидно всички множества от
елементарни събития от вида:
x-1(A)={w: x(w)О A},
където A е интервала (x,y) от реалната права ще са събития.
Произволен набор от сл.в. може да се разглежда като векторна
сл.в.
Теорема 4.5
Ако x е сл.в., то съответствието ''пълен праобраз''
x-1(.) прехвърля B в s-подалгебра
AxМ A, за елементите на която е определена
вероятността P.
Доказателство: Следствие от теорема 4.4.
Теорема 4.6
Ако определим вероятност върху B
по формулата Q(B)=P(x-1(B)), то тройката (R1, B,Q)
става вероятностно пространство.
Доказателство: За да докажем, че тройката (R1, B,Q)
става вероятностно пространство е достатъчно да проверим
аксиомите за вероятност.

Определение 4.7
Функцията f(· ): Rn ѕ® Rm се нарича
Борелова, ако пълният праобраз на Борелово множество е Борелово
множество.
Поради теорема 4.4 проверката за това дали една функция
е Борелова е тривиална -- достатъчно е да проверим дали пълният
праобраз на интервал е Борелово множество.
Теорема 4.7
Борелова функция от (векторна) сл.в. е (векторна) сл.в.
Доказателство: Достатъчно е да разгледаме съответствието
x = f(x(w)). Пълният му праобраз може да се запише като
композицията x-1(f-1(.)) .

Доказателство: (Теорема 4.3)
Така за да я докажем е достатъчно
да проверим, че функциите x+y, x y са Борелови. Да разгледаме,
например, x+y и множеството: A={ x+y< c}М R2. Да
разгледаме изброимото обединение на двумерни интервали:
B = Иi ( {x: x < xi}З {y:y < yi}).
(4.1)
Тук с (xi,yi) сме
означили всички двойки рационални числа такива, че xi+yi<c .
Очевидно AЙ B . Обратно, за всяка двойка (x,y): x+y<c
интервалът (x,c-y) е непразен и в него съществува
рационално число -- да го означим с a. Имаме a+y<c.
Сега интервалът (y,c-a) е непразен и в него съществува
рационално число -- да го означим с b. При това са изпълнени и
трите неравенства a+b<c, x<a, y<b. 
Теорема 4.8
Съществува взаимно еднозначно съответствие между функциите на
разпределение и възможните вероятности, определени
на B в R1.
Доказателство: Следва от това, че всяка вероятност се определя от своите
стойности върху пораждащите Бореловата алгебра интервали.
Д.Въндев -Теория на вероятностите - January 9, 2002



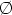 ,
когато i№ k или j№ l.
,
когато i№ k или j№ l.


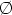 ,
когато i№ k или j№ l.
,
когато i№ k или j№ l.
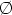 ,
И Hi=W.
Да определим простата сл.в.
xn(w)=ai, wО Hi . Тогава
|x(w)-xn(w)|Ј2C/n.
Значи x(w)= lim xn(w).
,
И Hi=W.
Да определим простата сл.в.
xn(w)=ai, wО Hi . Тогава
|x(w)-xn(w)|Ј2C/n.
Значи x(w)= lim xn(w). Доказателството на тази теорема изисква известна математическа подготовка
и ще бъде дадено в последната секция.
Доказателството на тази теорема изисква известна математическа подготовка
и ще бъде дадено в последната секция.







