Предишна тема Съдържание Следваща тема

Тема 11   Трансформации на случайните величини



Ще изведем формулата за пресмятане на плътността при аналитична трансформация на непрекъсната сл.в. и ще я приложим за редица разпределения.

11.1   Смяна на променливите

Теорема 11.1   Нека U:Aѕ® B, където A,BО Rn са отворени множества, U e взаимноеднозначно съответствие и V=U-1. Нека функцията V(x) притежава непрекъснати производни в B. Нека x е сл.в. със стойности в A и тя има плътност fx(x) за xО A. Тогава сл.в. h=U(x) има плътност fh(y), която се задава по формулата:
f
 
h
(x)=|J(V)(x)|f
 
x
(V(x))  за   xО B,     (11.1)
където с J(V) е якобианът на трансформацията V, т.е. детерминантата на матрицата:

м
п
п
п
п
п
н
п
п
п
п
п
о
V1
x1
V1
x2
...
V1
xn
V2
x1
V2
x2
...
V2
xn
... ... ... ...
Vn
x1
Vn
x2
...
Vn
xn
ь
п
п
п
п
п
э
п
п
п
п
п
ю		 .

Тази теорема няма да доказваме -- тя е следствие от стандартните теореми на анализа за смяна на променливите под знака на интеграла.

Пример 11.1   Многомерно нормално разпределение

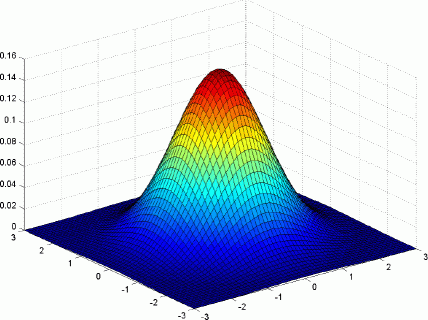Плътността на стандартното нормално разпределение N(0,I) в Rn има вида:
f(
x
 
) =
n
P
i=1
1
(2p )1/2
e
-xi2/2
 
=
1
(2p )n/2
e
-||
x
 
||2/2
 
,
където x О Rn.
Фигура 11.1: Нормално N(0,I) в R2

Нека сл.в. xО N(0,I). Ще разгледаме линейната трансформация h = Ax + b. Тук A е неизродена n n матрица, а bО Rn. Тогава плътността на h ще се изчисли по формулата (11.1).

f
 
h
(x)=|J(V)|f
 
x
(V(x))=
|A-1|
(2p )n/2
e
-
1
2
(x-b)'(AA')-1(x-b)
 
.
Като означим матрицата C=AA', получаваме стандартния вид на многомерното нормално разпределение N(b,C) с параметри E h=b и cov(h)=C:

f(x,b,C)=
1
|C|1/2(2p )n/2
e
-
1
2
(x-b)'C-1(x-b)
 
.     (11.2)

Да проверим тези равенства за параметрите:
E h = AE x+b = b,   cov(h)=E (h-b)(h-b)'=A(E xx')A'=AA'.

11.2   Конволюция на плътности

Ще приложим формулата 11.1 към следната задача:

Теорема 11.2   Нека са дадени две независими сл.в. x и h с положителни плътности на разпределение. Тогава са изпълнени следните формули:
f
 
x + h
(x) =
Ґ
у
х
-Ґ
f
 
x
(x-y)f
 
h
(y) dy
Ако   x,h > 0,то f
 
x * h
(x) =
Ґ
у
х
-Ґ
1
y
f
 
x
(x/*y)f
 
h
(y) dy
Ако   x,h > 0,то f
 
x / h
(x) =
Ґ
у
х
-Ґ
y f
 
x
(x*y)f
 
h
(y) dy


Доказателство: Да докажем формула (11.3). Разглеждаме двумерната сл.в. {x,h} . Тя има плътност f(x,y) =fx(y)fh(y) защото двете сл.в. са независими. Нека разгледаме сега трансформациите:
U= м
н
о
u = x + y,
v = y
   и    V = U-1 = м
н
о
x = u - v,
y = v
и приложим формула (11.1). Тъй като якобианът на V е равен на 1, получаваме за двумерната плътност на U({x,h}) формулата:
f(u,v) = f
 
x
(u-v)f
 
h
(v).
За да получим плътността на първата сл.в. x+h, трябва да интегрираме по втората променлива y. Формули (11.4) и (11.5) се доказват аналогично.

11.3   Гама и Бета разпределения

Тук ще се запознаем накратко с две много популярни семейства разпределения.
Определение 11.1   Наричаме Гама-разпределение G(a,l) разпределение с плътност:
f(x)=
la
G(a)
xa-1 e
-l x
 
,   x > 0 .     (11.3)

Това семейство е популярно в статистиката, защото е тясно свързано с нормалното. При стойности на a кратни на 1/2 е известно като Хи-квадрат разпределение и описва разпределението на сума от квадрати на центрирани независими еднакво нормално разпределени сл.в.
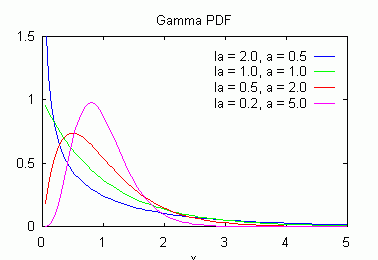
Фигура 11.2: Гама разпределение

Параметърът a, който определя формата му, има смисъла на степени на свобода - колкото по-голям е, толкова по-неопределени са стойностите на сл.в. Гама-разпределението има винаги положителна асиметрия, но тя клони към нула при нарастване на a. Вторият параметър l е мащабен -- той не оказва влияние на ексцеса и асиметрията. При a Ґ центрираното и нормирано Гама-разпределение клони към нормалното. Математическото му очакване е µ = a / l а стандартното отклонение - s = (a)1/2 / l.

Определение 11.2   Наричаме Бета разпределение с плътност:
f(x)=
1
B(a,b)
xa-1(1-x)b-1,   0<x<1.     (11.4)

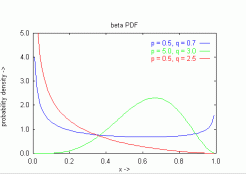Тук с B(a,b) сме означили Бета-функцията.

На фиг.11.3 са показани три различни плътности от семейството на Бета разпределенията. Вижда се, че те могат да имат различна по знак асиметрия. С нарастването на параметрите a и b, разпределението се изражда (дисперсията му клони към 0). Ако скоростта на нарастване е еднаква и то е правилно нормирано, Бета разпределението също клони към нормалното.
Фигура 11.3: Различни Бета разпределения

Ще приложим формулата (11.1) за да опишем връзката между Гама и Бета разпределенията.

Теорема 11.3   Нека xОG(a,l) и hОG(b,l) са независими Гама - разпределени сл.в. Тогава
  1. сл.в. z=x+h О G(a+b,l);
  2. сл.в. q=x/x+h О B(a,b);
  3. сл.в. q^z.
Доказателство: Разпределението на двумерната сл.в. {x,h} е
f(x,y) =
la
G(a)
xa-1 e
-l x
 
lb
G(b)
yb-1 e
-l y
 
.
Да разгледаме сега трансформациите:
U= м
п
н
п
о
u = x + y,
v =
x
x+y
   и    V = U-1 = м
н
о
x = uv,
y = u*(1-v)
и приложим формула (11.1). Тъй като якобианът на V е равен на u, получаваме за двумерната плътност на {z,q} формулата:
f(u,v) = (
la+b
G(a+b)
ua+b-1 e
-l u
 
) (
G(a+b)
G(a)G(b)
va-1 (1-v)b-1),
откъдето следват всички твърдения на теоремата.
Д.Въндев -Теория на вероятностите - January 9, 2002
Предишна тема Съдържание Следваща тема