Предишна тема Съдържание Следваща тема

Тема 12   Видове сходимост на редици сл.в.



Всъщност в по - голямата си част това е тема от математическия анализ. Видовете сходимост се разделят на две големи групи. Първата група касае само разпределенията на сл.в. и следователно, породените от тях мерки върху бореловата s-алгебра. По традиция от тази група сходимости в теория на вероятностите се изучава само една --- тази по разпределение.

Втората група сходимости е по - богата и значително по - използувана. Тук влизат всички сходимости на сл.в., или измерими функции върху абстрактно пространство с мярка.

12.1   Сходимост на разпределения на сл.в.

Определение 12.1   Казваме, че редицата от функции на разпределение Fn е сходяща към функцията на разпределение F, ако редицата от числа Fn(x) клони към числото F(x) за всяко x, което е точка на непрекъснатост на F.

Определение 12.2   Казваме, че редицата от характеристични функции fn е сходяща към характеристичната функция f, ако редицата от комплексни числа fn(t) клони към числото f(t) за всяко t.

Определение 12.3   Казваме, че редицата от функции на разпределение Fn клони слабо към функцията на разпределение F, ако за всяка ограничена непрекъсната функция f е в сила сходимостта:
у
х
Ґ


-Ґ
f(x) dFn(x) ѕ® у
х
Ґ


-Ґ
f(x) d F(x).

Теорема 12.1   Определенията 12.1, 12.2 и 12.3 са еквивалентни.

Доказателство: Ще докажем еквивалентността на горните дефиниции в следния ред:

12.1 12.3 12.2 12.1
Първата стрелка. Нека Fn(x)ѕ® F(x) във всяка точка на непрекъснатост на F. Нека f(x) е ограничена и непрекъсната - |f(x)|<C.
1. Съществува L>0, такова, че F(L)-F(-L)>1-e/C. Тогава |т|x|<L f(x) d F(x) -т-ҐҐf(x) d F(x)| < 2e и за n>N |т|x|<L f(x) dFn(x) -т-ҐҐf(x) dFn(x)| < 4 e .
2. В интервала [-L,L] съществуват краен брой k точки на непрекъснатост x0=-L<x1< ... < xk=L на F, такива, че supxi-1Ј x Ј xi |f(x)-f(xi)|<e . Тогава |т|x|<L f(x) d F(x) - Si=1k f(xi) (F(xi)-F(xi-1))| <e.
3. Остана да се използува, че supi=1k |Fn(xi)-F(xi)|   0 .

Втората стрелка е тривиална. Функцията ei x t е ограничена и непрекъсната по x при всяко фиксирано t.

Третата стрелка не е тривиална. Тя следва от формулата за обръщане (9.4) на х.ф.

12.2   Сходимости на сл.в.

Определение 12.4   Казваме, че редицата от сл.в. xn е сходяща към сл.в. x по разпределение, ако Fn клони към F във всяка точка на непрекъснатост на F . Ще означим тази сходимост по следния начин:
xn
d
ѕ®
 
x
.

Определение 12.5   Казваме, че редицата от сл.в. xn е сходяща към сл.в. x по вероятност, ако за всяко e > 0
P  (|xn-x| > e ) ѕ® 0.
Ще означим тази сходимост по следния начин:
xn
p
ѕ®
 
x.

Определение 12.6   Казваме, че редицата от сл.в. xn е сходяща към сл.в. x в средно от степен r, ако
E  |xn-x|r ѕ® 0.
Ще означим тази сходимост по следния начин:
xn
r
ѕ®
 
x.

Определение 12.7   Казваме, че редицата от сл.в. xn е сходяща към сл.в. x почти сигурно (или с вероятност 1), ако
P  ( |xn-x| ѕ® 0 )=1.
Ще означим тази сходимост по следния начин:
xn
п.с.
ѕ®
 
x.

Между различните видове сходимост съществуват естествени връзки отразени на фиг. 12.1. Стрелките показват от коя от сходимостите следва друга.



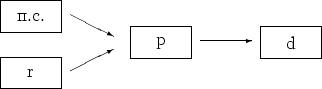
Figure 12.1: Сходимости на редици сл.в.

Теорема 12.2   Диаграмата на фиг.12.1 е вярна.

Доказателство:
Сходимост п.с. влече сходимост по вероятност. Да означим с Anr събитията Anr={w:|xn-x|>1/r}. Достатъчно е да покажем, че за всяко цяло r>0 имаме P  (Anr)   0 при n  Ґ. От друга страна имаме представянето:

{w:xn  x}=
Ґ
З
r=1
Ґ
И
n=1
Ґ
З
m=n
_
A
 
mr.

Тъй като вероятността на това събитие е 1, то неговото допълнение ще има нулева вероятност.

0=P   (
Ґ
И
r=1
Ґ
З
n=1
Ґ
И
m=n
Amr)= P   (
Ґ
З
n=1
Ґ
И
m=n
Amr)= P   (
Ґ
З
n=1
Bnr) .
Но събитията Bnr=Иm=nҐAmr образуват намаляваща редица. Тогава от аксиомата за непрекъснатост следва, че P  (Bnr)   0 и следователно P  (Anr)   0.
Сходимост в средно r влече сходимост по вероятност. Това твърдение следва директно от неравенството на Чебишов:
P  (|xn-x|r > e ) Ј
E  |xn-x|r
er
.

Сходимост по вероятност влече сходимост по разпределение. Да означим с An={xn-e <x <xn+e}. При това P  (An)   1. Функцията на разпределение на xn може да се запише по формулата за пълната вероятност в вида:
Fn(x)=P  (xn < x) = P  (An)P  (xn < x|An) +P   (
_
A
 
n)P   (xn < x|
_
A
 
n).

Ще оценим отгоре и отдолу Fn(x):
Fn(x) Ј
P  ({xn < x} З An) +P   (
_
A
 
n)
=
P  ({xn<x} З{x-e <xn} З {xn <x+e}) +P   (
_
A
 
n)
Ј
P  ({x < x+e} З {xn <x+e}) +P   (
_
A
 
n)
Ј
P  ({x < x+e}) +P   (
_
A
 
n).
При преминаването втория към третия ред използуваме съотношението:
{x-e <xn}З {xn<x}М {x-e <x}= {x < x+e}.
От доказаното неравенство следва, че limsup Fn(x) Ј F(x+e).

Да разгледаме сега обратното неравенство.
Fn(x) і P  ({xn < x} З An)
= P  ({xn<x} З{x-e <xn} З {xn <x+e})
і P  ({x < x-e} З{x-e <xn} З {xn <x+e}) =P  (BЗ An),
където B={x < x - e}. Сега използувахме обратното включване:
{x<x-e}З{xn <x+e}М {xn<x}.
Тъй като P  (An)   1, то P  (BЗ An)   P  (B). От тук следва, че
liminf Fn(x) і F(x-e). Тъй като и двете неравенства са изпълнени за всяко e, от тях следва равенството lim Fn(x) = F(x) за всяка точка на непрекъснатост на F(x).

12.3   Контрапримери

Пример 12.1   Сходимост по разпределение не влече сходимост по вероятност.
Да разгледаме сл.в. x приемаща стойностите 1 и -1 с равни вероятности и редицата: xn= (-1)n x. Всички разпределения са еднакви, но P  (|xn-x|>e) не клони към 0.

Има и едно изключение, когато сходимостта по разпределение влече сходимост по вероятност --- когато граничната сл.в. е константа. Докажете го.

Пример 12.2   Сходимост по вероятност не влече сходимост п.с.
Ще конструираме редицата от последователни групи сл.в. n-тата група ще се състои от 2n сл.в. Да си представим, че вероятностното пространство е интервала [0,1) с мярка на Лебег. За да конструираме n-тата група ще го разделим на 2n равни подинтервала (затворени от ляво). Сл.в. от групата приемат стойности 1 за точно един подинтервал и нула навсякъде другаде. Така P  (|xn|>e)  0 и редицата клони по вероятност към константата 0. За всяко конкретно w, обаче, съществуват безбройно много членове на редицата със стойности по - големи от e, т.е. тя не е сходяща п.с.

От всяка редица сходяща по вероятност, може да се извлече подредица сходяща п.с. към същата гранична сл.в. Докажете това.

Пример 12.3   Сходимост по вероятност не влече сходимост в средно r.
Сходимостта на редицата по вероятност към 0 в пример 12.2 не зависи от стойностите на величините, когато са различни от 0. Значи, ако умножим сл.в. от n-тата група с 2n/r ще получим, че E  (|xn|r)=1, което означава, че редицата не е сходяща към 0 в средно, но остава сходяща по вероятност.

Пример 12.4   Сходимост п.с. не влече сходимост в средно r.
Достатъчно е да разгледаме подредица на редицата от пример 12.3, която е сходяща п.с. Това могат да бъдат, например, последните (най - десни) сл.в. от всяка група. Тук, както и в предния пример, сходимостта п.с. не зависи от стойностите им. Сходимостта в средно, обаче е нарушена.

Когато една редица сл.в. е ограничена и сходяща п.с., то тя е сходяща и в средно. Докажете го.

Пример 12.5   Сходимост в средно r не влече сходимост п.с.
Редицата от пример 12.2 има такова поведение. Проверете го.
Д.Въндев -Теория на вероятностите - January 9, 2002
Предишна тема Съдържание Следваща тема