Предишна тема Съдържание Следваща тема

Тема 7   Нормално разпределение

В тази лекция си поставяме следните цели:

7.1   Нормално разпределение

Определение 7.1   Казваме, че сл.в. с непрекъснато разпределение е нормално разпределена N(µ,s), ако нейната плътност има вида:
f(x,µ ,s ) =
1
(2p)1/2s
e
-(x-µ )2/2s 2
 
.     (7.1)
Математическото очакване на това разпределение е µ, а дисперсията му е s2. Стандартно нормално разпределение се нарича разпределението N(0,1), неговата плътност означаваме с f(x).
Фигура 7.1: Стандартно нормално

Нормалното разпределение има голямо значение в теория на вероятностите и математическата статистика, което се дължи на твърдението, известно като Централна Гранична Теорема. То гласи, че разпределението на сума от голям брой независими, еднакво разпределени случайни величини клони към нормално разпределение.

7.2   Теореми на Муавър-Лаплас

Тук ще се опитаме да покажем как е възникнала формулата за плътността на нормалното разпределение.

7.2.1   Локална теорема

Нека устремим към безкрайност броят на опитите в схемата на Бернули. Да означим
x =
k - np
(n p q)1/2
и поискаме това число да остане ''почти постоянно'' при n Ґ. Смисълът на това число е ясен - това е центрираната и нормирана стойност на сл.в. брой на успехи. Ясно е, че тогава (при фиксирана вероятност за успех p) също и k Ґ. Да означим s= (n p q)1/2.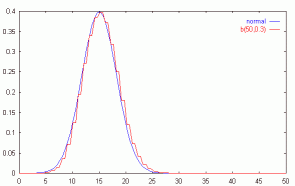
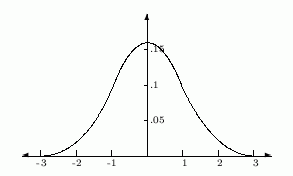
Теорема 7.1  (Локална теорема на Муавър-Лаплас) Нека p,x са фиксирани. Нека n   Ґ Нека означим sn2 = n p q , kn = n p + sn x. Тогава равномерно в интервала -Ґ<a<x<b<Ґ е изпълнено съотношението:
sn b(n,kn,p) ѕ® f(x)
Фигура 7.2: Нормална апроксимация на биномно разпределение


Доказателство: За простота ще изпускаме индекса от означенията sn, kn в доказателството. Да логаритмуваме биномната вероятност от лявата страна
ln b(n,kn,p)= ln n! - ln kn! - ln (n-kn)! + kn ln p + (n-k) ln q.     (7.2)
Ще използуваме представянето на Стирлинг на ln n!:
ln n! = n ln n +
1
2
ln (2p n) - n + a(n),     (7.3)
където a(n)= O(1/n). Да означим mn=n-kn. Тъй като mn, kn   Ґ, то от (7.2 ) и (7.3) следва
ln b(n,k,p)-
1
2
ln 2p
=nln n - kln k - mln m + kln p + mln q -
1
2
ln
k m
n
+ bn=
=- (np+s x)ln(1+
x q
s
) - (n q-s x)ln (1-
x p
s
) -
1
2
ln
k m
n
+ bn,
където bn=a(n) - a(kn)-a(mn)=O(1/n), k=np+s x и m=n-k= n q-s x. Тук ще се отклоним малко да разгледаме дробта:

km
ns2
=
(np+s x)(n q-s x)
ns2
= (1+
(q-p)x
s
-
pqx2
s2
).

Така лесно ще можем да получим израз за третия логаритъм в (7.4) чрез s.

1
2
ln
m k
n
=
1
2
lns + O(
1
s
).

За първите два логаритъма ще използуваме разложението ln(1+x)= x-x2/2 + O(x3). Заместваме, съкращаваме и получаваме окончателно:
lns+ ln b(n,kn,p)=
1
2
ln 2p+
- (np+s x)(
x q
s
-
x2 q2
2s2
)) - (n q-s x)(-
x p
s
-
x2 p2
2s2
)) +gn
=
1
2
ln 2p-
x2
2
+gn.
където gn=O(s-1)=O(n-1/2).

И тази теорема може да се уточни, както теоремата на Поасон, но тук няма да се спираме на това. Тя ни дава възможност да пресмятаме лесно конкретни биномни вероятности. При големи стойности на n това са твърде малки числа.

7.2.2   Интегрална теорема

За да можем да пресмятаме суми от Биномни вероятности си служим със следната интегрална теорема на Муавър - Лаплас.

Теорема 7.2   Да означим с x биномна сл.в. с разпределение b(n,k,p). Тогава при фиксирани b,a,p имаме
P (b<
x - np
(n p q)1/2
< a) =
[np + a (n p q)1/2]
S
k=[np + b (n p q)1/2]
b(n,k,p)
 
 
ѕ®
 
n Ґ
у
х
a


b
f(y) dy.


Доказателство: За краен интервал (b,a) тя лесно следва от локалната теорема, а за произволен -- от централната гранична теорема за еднакво разпределени събираеми.

7.3   *Доверителен интервал за вероятност

В този параграф ще се запознаем с един статистически извод --- твърдение за неизвестното разпределение на стойностите в изучавано множество от обекти въз основа на ограничената информация получена от една случайна крайна извадка.

Нека си поставим за цел по n наблюдавани стойности да кажем нещо за неизвестната вероятност p на поява на даден признак. Нека с k означим резултата от нашите наблюдения -- броят на поява на признака в извадката. Ако предположим, че извадката е случайна и изучаваното множество толкова голямо, че да се пренебрегне възможността от повторение на вече изтеглен обект, то можем да гледаме на резултатите - появата на признака в поредния обект като на независими сл.в. Следователно общия брой появи k е подчинен на биномно разпределение.

Ще използуваме интегралната теорема на Муавър -- Лаплас (теорема 7.2).
у
х
x


-x
f(y) dy= P (-x<
k - np
(n p q)1/2
< x) = P (|
k
n
-p|<x (pq/n)1/2).
Можем да подберем числото x=1.96, тогава вероятността е 0.95. Тъй като max(pq)=1/4, получаваме:
0.95 Ј P (|
k
n
-p|<
1.96
2 n1/2
).

С други думи горното неравенство ни казва: Ако сте наблюдавали определена стойност на k при известен брой на експериментите n, то с вероятност по-голяма от .95 можете да твърдите, че неизвестната стойност на вероятността не е много далече от честотата. При това големината на доверителния интервал е от порядъка на 1/(n)1/2. Смисълът на надежността на вашето твърдение е следния:

При многократно повторение на целия опит и изработване на вашето заключение в 95 процента от случаите вие ще сте прави -- неизвестната вероятност ще се покрива от така получения интервал.

7.4   *Формула на Стирлинг

7.4.1   Просто доказателство

Да разгледаме интеграла:

n!= у
х
Ґ


0
xn e-x dx.     (7.4)
Ще направим смяна на променливите:
xn e-x= nn e-n e
-t2
 
.     (7.5)

Тъй като подинтегралната функция има максимум при x=n>0 , променливата t ще се мени в интервала -Ґ,Ґ. За да изразим dx ще логаритмуваме 7.6 и ще го диференцираме:

n lg x - x = - t2 +nlg n -n,     (7.6)
dx =
2 t
x
x-n
dt
    (7.7)

За да изразим tx/(x-n) само чрез t да отбележим, че

t2=x-n-nlg
x
n
=n (z-lg(1+z)),   z=
x-n
n

Ще представим lg(1+z) по формулата на Тейлор до 2-ри ред:

lg(1+z) = z -
z2
2
1
(1+zq(z))2
,
където 0<q(z)Ј 1. Значи (t и z имат еднакъв знак)
t2=
n
2
z2
(1+zq(z))2
,   t =(
n
2
)1/2
z
1+zq(z)
,   z-1+q(z)=(
n
2
)1/2t-1.     (7.8)
Сега можем да изразим tx/x-n чрез t:
t
x
x-n
= t+
t
z
= (
n
2
)1/2 + t(1- q(z)).     (7.9)
Няма нужда да заместваме z, за нас е важно само че 0<1-q(z)<1. Така получаваме за интеграла 7.5:
n!=(2 n)1/2 nn e-n( у
х
Ґ


-Ґ
e
-t2
 
dt+ (
2
n
)1/2 у
х
Ґ


-Ґ
(1-q(z)) t e
-t2
 
dt.)     (7.10)
Първият интеграл е добре известният интеграл на Поасон и неговата стойност е (p)1/2, а вторият е ограничен. Така окончателно получаваме:
n!=(2p n)1/2 nn e-n( 1+ en),   en <
C
(n)1/2
.

7.4.2   Директно доказателство

Ще предполагаме известно разложението в ред на функцията ln(1+x):
ln(1+x)=x-
x2
2
+
x3
3
-... (-1)n-1
xn
n
...     (7.11)

От него лесно получаваме
ln(
1+x
1-x
)= ln(1+x)- ln(1-x)= 2x(1+
x2
3
+
x4
5
+ ...
x2m
2m+1
... )     (7.12)
Като поставим тук x=1/(2n+1) получаваме:
(n +
1
2
)ln (1+
1
n
)= 1+
(2n+1)-2
3
+
(2n+1)-4
5
+ ...
(2n+1)-2m
2m+1
...     (7.13)
Този израз може да се оцени от двете страни:
1<(n +
1
2
)ln (1+
1
n
)Ј 1+
1
3(2n+1)2
(1+ (2n+1)-2+...)= 1 +
1
12n(n+1)
.     (7.14)
Значи като експоненцираме и разделим на e ще получим неравенствата:
1<e-1(1+
1
n
)n+1/2<e
1
12n(n+1)
 
    (7.15)
От друга страна нека разгледаме редицата an= n!en n-(n+1/2). Тогава
an
an+1
=e-1(1+
1
n
)n+1/2     (7.16)
Значи

1 <
an
an+1
< e1/12n(n+1)=
e1/12n
e1/12(n+1)

Следователно, an>an+1 и an e-1/12n < an+1 e-1/12(n+1) и редицата клони към крайна граница a в интервала (0,1), като an e-1/12n < a < an. Значи съществува число qn в интервала (0,1), че a=an e-qn/12n. Следователно,
n! = a nn+1/2 e-n e
-
qn
12n
 
    (7.17)

Остава да се определи константата a=(2 p)1/2. Това също може да стане директно, но няма да го правим, тъй като вече го получихме в (7.11).


Д.Въндев -Теория на вероятностите - January 9, 2002
Предишна тема Съдържание Следваща тема