Предишна тема Съдържание Следваща тема

Тема 6   Дискретни разпределения



В тази лекция си поставяме за цел да обобщим и разширим понятията си за:

6.1   Пораждащи функции

Определение 6.1   Сл.в. приемаща за стойности натуралните числа наричаме целочислена.

Целочислените сл.в. са особено удобни за моделиране на реални явления като брой успехи или други бройки. За пресмятане на моментите на целочислени сл.в. служат т.н. пораждащи моментите функции.
Определение 6.2   Пораждащата функция на целочислена сл.в. x се задава с формулата:
p(s)
def
=
 
E   s
x
 
=
Ґ
S
i=0
si P  (xi=i)=
Ґ
S
i=0
si pi.     (6.1)
Пораждащата функция е удобна защото съществува винаги (при достатъчно малко s, например, когато s Ј 1) и е диференцируема при 0Ј s <1. Тя притежава още следните свойства:
Теорема 6.1   Между разпределенията на целочислени сл.в. и пораждащите функции съществува взаимно еднозначно съответствие.

Доказателство: Следва от формулата: p(n)(0)= n ! pn.

Биномно разпределение

Определение 6.3   Редица от независими еднакво разпределени случайни величини {xi, i=1,2,...}, всяка от които приема две стойности: 1 и 0 с вероятности (съответно) p и q=1-p, наричаме схема на Бернули.

Да разгледаме сумата hn на n сл.в. от схемата на Бернули. Това е целочислена случайна величина, приемаща стойности от 0 до n. Ние я интерпретираме като Брой успехи от n опита с постоянна вероятност p за успех във всеки опит. Разпределението на тази сл.в. наричаме биномно. Вероятността тази сл.в. да приеме стойност k наричаме биномна и означаваме с b(n,k,p).

Теорема 6.2   Биномните вероятности се пресмятат по формулата:

b(n,k,p) = ж
и
n
k
ц
ш		 pk qn-k     (6.2)
k=0,1,...,n
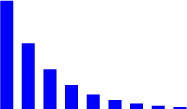
Фигура 6.1: Биномно разпределение n=7


Доказателство: Първо да пресметнем вероятността на събитието
W
 
e1,e2,...,en
=
n
З
i=1
{ xi=ei},
където ejО{0,1},   j=1,2,...,n. Тъй като сл.в. са независими и P(x=1)=p, получаваме
P  (W
 
e1,e2,...,en
)= p
n
S
i=1
ei
 
q
n-
n
S
i=1
ei
 
    (6.3)
Ако означим hn=Si=1nxi и k=Si=1nei, ще получим

P(hn=k)=
 
S
e1+e2+...+en=k
pk qn-k= pk qn-k
 
S
e1+e2+...+en=k
1.
Но от тук следва търсената формула.

Пораждащата функция на биномното разпределение се пресмята лесно, защото биномната сл.в. h е сума на еднакво разпределени независими сл.в.
E   s
h
 
=E  
n
P
i=1
s
xi
 
= (E   s
x1
 
)n= (ps+q)n.

Геометрично разпределение

Нека разгледаме в ситуацията на независими опити (схема на Бернули) сл.в. x --- брой успешни опити до първи неуспех.

Определение 6.4   Казваме, че целочислената сл.в. x има геометрично разпределение, ако:

P (x=m) = pm q,
m=0,1,2,....
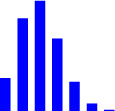
Фигура 6.2: Геометрично разпределение

Математическото очакване и дисперсията на това разпределение се пресмятат лесно:
E   x= q
Ґ
S
k=0
k pk = qp
Ґ
S
k=0
k pk-1= qp
d
dp
(
1
1-p
)=
p
q
,
D  x= E  x(x-1) + E x - (E  x)2= q
Ґ
S
k=0
k(k-1) pk +
p
q
- (
p
q
)2=
qp2
d2
dp2
(
1
1-p
)+
p
q
-(
p
q
)2= (
p
q
)2 +
p
q
.

Хипергеометрично разпределение

Да разгледаме една задача от статистическия качествен контрол. Нека е дадена партида съдържаща N изделия, от които M са дефектни. Правим случайна извадка от n<N изделия. Пита се каква е вероятността точно m от тях да са дефектни.

Оказва се, че разпределението на сл.в. брой дефектни е следното:
Определение 6.5   Казваме, че целочислената сл.в. x има хипергеометрично разпределение, ако:

P (x=m) =
ж
и
M
m
ц
ш		 ж
и
N-M
n-m
ц
ш
ж
и
N
n
ц
ш
,
m=0,1,...,n.
Фигура 6.3: Хипергеометрично N=100, M=20, n=10

Тази формула се извежда лесно. Броят на всички възможни извадки без връщане очевидно е
ж
и
N
n
ц
ш
(смятаме ги за равновероятни). ''Благоприятните'', тези които съдържат точно m дефектни детайла, могат да се получат чрез комбиниране на извадка от M на m дефектни и извадка от N-M на n-m изправни. Тъй като извадките от здрави и дефектни детайли се комбинират без ограничения, общият брой на ''благоприятните'' извадки става
ж
и
M
m
ц
ш		 ж
и
N-M
n-m
ц
ш		 .

Математическото очакване и дисперсията на това разпределение също се пресмятат лесно:
E  x= n p,   p=
M
N
,   q=1-p
D  x= n p q
N-1
N-n
.
От тези формули се вижда, че това разпределение клони към биномното при голям брой N на детайлите в партидата.

Разпределение на Поасон

Поасоновото разпределение се определя лесно като граница на биномни разпределения, когато n Ґ така че n p l>0. Сл.в. може да приема всякакви целочислени стойности:
P  (x = k) = e
-l
 
lk
k !
.     (6.4)
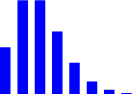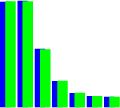
Фигура 6.4: Поасоново разпределение

То е особено подходящо за моделиране на броя на случайни редки събития -- брой частици на единица обем, брой радиоактивни разпадания за единица време и т.н. Средното и дисперсията му съвпадат: E x= D x= l. Това най-лесно се вижда от пораждащата функция на Поасоновото разпределение, която се пресмята директно:
E   s
h
 
=e
-l
 
Ґ
S
k=1
(l s)k
k !
= e
l(s-1)
 
.

6.2   Близости между дискретни разпределения

Апроксимациите играят съществена роля в теория на вероятностите. Много от получените формули са тежки за пресмятане и се налага те да бъдат замествани с приближени.

Поасоново и биномно

Тук ще разгледаме едно много полезно и старо приближение на биномната вероятност при малки k.

Теорема 6.3   (Теорема на Поасон) Ако в схемата на Бернули n pn   l, то

b(n,k,pn)
 
n pn = l
ѕ®
 
n Ґ
lk
k!
e
-l
 
.
Фигура 6.5: Поасонова апроксимация n=100,p=0.01


Доказателство: Да означим l=n p. Можем да запишем биномната вероятност във формата:
b(n,k,p) =
n(n-1)... (n-k+1)
k!
pk(1-p)n-k =
lk
k!
e
-l
 
e(k,n,l),
където
e(k,n,l)=
k-1
P
i=0
(1+
i
n
)     (1-
l
n
)k       e
l
 
(1-
l
n
)n .

Всеки от трите съмножителя на дясната страна клони към 1 при фиксирано k и n pn  l .

Още по-лесно се доказва тази теорема с помощта на пораждащи функции. Наистина, достатъчно е да покажем, че

(ps+q)n = (1+
(s-1)l
n
)n   e
l (s-1)
 
.

Възниква въпросът колко точно е приближението на Поасон. Ще приведем едно уточнение взето от [(А.А.Боровков,1972)].
Теорема 6.4   (Уточнение) Нека kЈ 1+ n/4 и p < 1/4 . Тогава
k
n
l +
7 k (1-k) - 8 l2
12 n
Ј ln e(k,n,l) Ј
k
n
l +
k (1-k)
n
    (6.5)

Доказателство: Да логаритмуваме израза в (6.5)
ln e(k,n,l)= (
k
S
i=0
ln (1-
i
n
) + ((n-k) ln(1-
l
n
) + l).     (6.6)
Да се възползуваме от неравенствата за ln(1-x) при 0Ј x Ј 1/4:
-
7x
6
Ј - x(1+
x
2(1-x)
)Ј ln(1-x)Ј -x,
ln(1-x)-x і -
x2
2(1-x)
і -
2x2
3
.

Сега лесно получаваме:
ln e(k,n,l)Ј -
k-1
S
i=1
i
n
-(n-k)p + np=
k
n
l +
k (1-k)
n
ln e(k,n,l)і -
7
6
k-1
S
i=1
i
n
+kp-n
2p2
3
=
k
n
l +
7 k (1-k) - 8 l2
12 n
.

Следователно, относителната грешка при използуването на формулата на Поасон за приближение на биномната вероятност не превъзхожда

k
n
l +
k (1-k)
n
.     (6.7)

От същите разсъждения следва, че при необходимост може да бъде получено и още по-добро приближение по формулата:

b(n,k,p) @
lk
k!
e
-l+
k
n
l +
k (1-k)
n
 

Хипергеометрично и биномно

Вече видяхме, че моментите (м.о. и дисперсията) на хипергеометричното разпределение апроксимират при N   Ґ тези на биномното разпределение. Тук ще покажем, че това е верно и за вероятностите.

Теорема 6.5   Нека N Ґ и M=p N. Тогава

ж
и
M
m
ц
ш		 ж
и
N-M
M-m
ц
ш
ж
и
N
n
ц
ш
 
 
ѕ®
 
N Ґ
b(n,m,p)     (6.8)
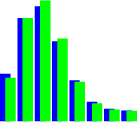
Фигура 6.6: Хипергеометрично и биномно (N=100,p=0.2)

Доказателство: Да прегрупираме лявата част:

ж
и
M
m
ц
ш
ж
и
N-M
n-m
ц
ш
ж
и
N
n
ц
ш
=
ж
и
n
m
ц
ш
M
N
M-1
N-1
...
M-m+1
N-m+1
N-M
N-m
N-M
N-m-1
...
N-M-n+m+1
N-n
ѕ® ж
и
n
m
ц
ш		 pm (1-p)n-m.

* Случайна сума сл.в.

Нека разгледаме редицата от целочислени независими еднакво разпределени сл.в. { xi, i=1,2,... }. Нека освен това ни е зададена независимата от тях сл.в. n. Нека разгледаме случайната величина h случайна сума от случайни събираеми:
h =
n
S
i=0
xi
и се запитаме какво е нейното разпределение и други числови характеристики. Тази задача се решава изключително елегантно с апарата на пораждащите функции.

Теорема 6.6   Нека сл.в. { xi, i=1,2,... } са независими с пораждаща функция p(s). Нека освен това независимата от тях сл.в. n има пораждаща функция q(s). Тогава пораждащата функция на h е равна на ph(s)=q(p(s)).

Доказателство: Наистина, да приложим формулата за пълната вероятност и условното м.о.:
p
 
h
(s)=E   s
n
S
i=0
xi
 
=
Ґ
S
k=0
P (n=k)E  ( s
k
S
i=0
xi
 
|n=i))=
Ґ
S
k=0
P (n=k)E  ( s
k
S
i=0
xi
 
))=
Ґ
S
k=0
P (n=k) p(s)k =q(p(s)).

Д.Въндев -Теория на вероятностите - January 9, 2002
Предишна тема Съдържание Следваща тема