|
Задача:
|
В n-мерно
Евклидово пространство E
са
дадени два единични ортогонални
|
вектора a
и b
, т.е. |a|=1,
|b|=1
и (a,b)=0
и изображение
|
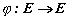
|
, което е
|
определено
по следния начин:
|
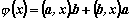
|
за всеки вектор
|
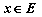
|
.
|
Да се
|
докаже,
че
|
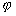 |
е симетричен
оператор в E
и че |
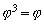
|
.
|
Решение:
 | Ще докажем, че |
|
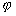 |
е симетричен оператор: |
 |
Първо
-че оператора е линеен |
|
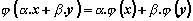 |
|
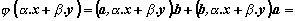 |
|
Първото
равенство е в сила, защото скаларното
произведение в линейно по всеки
множител. |
|
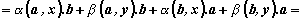 |
|
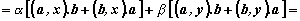 |
|
|
|
|
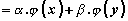 |
|
|
|
|
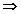 Операторът е линеен.
Операторът е линеен. |
|
|
|
 |
След
това - условието за
симетричност. |
|
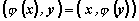 |
: |
|
|
|
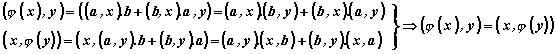 |
|
|
Използваме, че
скаларните произведения като |
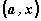 |
са числа и |
|
|
затова ги
изнасяме като множители пред
произведенията. |
| От горните две точки следва, че |
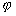 |
е симетричен оператор. |
 | Да докажем, че |
|
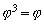
|
: |
|
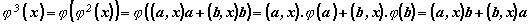 |
| По този начин получихме, че |
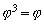
|
. |

|
за проекта
за темата
за
автора
e-mail
симетричен оператор - свойства
симетрични матрици
собствени вектори
канонизация
![]()
