симетричен оператор - свойства симетрични матрици собствени вектори канонизация

Симетрични матрици

В тази страница ще се запознаем с

	определение за симетрична матрица и основни примери;
	Свойството 1,че симетричните матрици образуват подпространство на пространството на всички квадратни оператори
	Свойство 2 и свойство 3 за обратна матрица и произведение на симетрични матрици.
	Свойство 4 , чрез което можем да получаваме симетрична матрица от произволна матрица.
	Задача за упражнение.

Определение за симетрична матрица:

Една квадратна матрица A

се нарича симетрична, ако е изпълнено

за

произволни стойности на индексите

Примери на симетрични матрици:

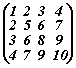С други думи една квадратна матрица A е симетрична, точно когато съвпада със своята транспонирана, т.е. A=A^t.Това условие по-лесно се проверява отколкото условието от определението.

Свойства на симетричните матрици:

Свойство 1:
Нека A и B са симетрични матрици, т.е.			и		, тогава:

е симетрична матрица

, защото

е симетрична матрица

, защото

Това свойство означава, че множеството от всички симетрични матрици от фиксиран ред образуват подпространство на пространството от всички квадратни матрици от този ред .

Свойство2 :
Ако матрицата A	е обратима и симетрична, то и нейната обратна		е симетрична.

Доказателство:

Нека да бележим с B обратната матрица

, тогава от

имаме:

От това равенство се вижда, че

също е обратна

матрица за A , но всяка обратима матрица има единствена обратна, то

е симетрична матрица.

Свойство 3
Ако две симетрични матрици A и B комутират помежду си ( A.B=B.A), то тяхното произведение също е симетрична матрица.

Доказателство:

Пример: Да разгледаме следните симетрични матрици

A и B не комутират и произведението им

не е симетрична матрица

матриците A и C комутират и за тях имаме

Като използвате, че		опитайте се да докажете следното свойство,
чрез което можем да получаваме симетрични матрици.