за проекта за темата за автора e-mail  

симетричен оператор - свойства симетрични матрици собствени вектори канонизация

Метод за канонизация на симетрични оператори

В тази страница са дадени:
Решени задачи за канонизация
задача 1 - оператор с прост спектър;
задача 2 - оператор с кратен характеристичен корен;
задача 3 - канонизация на симетрична матрица.
задачи за самостоятелно работа - зад 4, зад 5, зад 6 .

Задача 1:

Спрямо ортонормиран базис e1,e2,e3  на тримерно Евклидово пространство E е зададен линеен оператор  φ по следния начин: 

Да се намери ортонормиран базис на пространството, в който оператора  има диагонална матрица, както и тази диагонална матрица.
Решение:
Първо намираме матрицата A на оператора φ в дадения базис. Матрицата на оператора е симетрична и по доказана теорема следва, че оператора е симетричен:
След това пресмятаме характеристичния полином на намерената матрица:
След това намираме корените на характеристичния полином

За λ1=0 намираме решенията на системата Ax=0, където x е стълб с трите неизвестни 

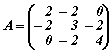Решението на тази система е едномерно и едно ненулево решение е c1=(2,2,1)  откъдето получаваме че, всички  собствени вектори със собствена стойност 0 са пропорционални на a1=2e1+2e2+e3.
За λ2=3 намираме решенията на системата (A-3E)x=0: 

Решение на тази система е c2=(2,-1,-2) и всички  собствени вектори със собствена стойност 3 са пропорционални на a2=2e1-e2-2e3.
За λ2=6 намираме решенията на системата (A-6E)x=0: 

Решение на тази система е c3=(1,-2,2) и всички  собствени вектори със собствена стойност 6 са пропорционални на a3=e1-2e2+2e3.
Получените вектори a1 , a2 и  a3 са  собствени за за различни собствени стойности  и доказахме теорема, че те са ортогонални. Нормираме ги за да получим ортонормиран базис от собствени вектори на φ :
аналогично получаваме:
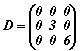Векторите от новия базис са собствени за оператора и матрицата на φ в този базис е D:

Задача 2: 

Спрямо даден ортонормиран базис  на тримерно линейно пространство  линеен оператор  φ има  матрица A. Да се намери ортонормиран базис на пространството, в който оператора  има диагонална матрица, както и тази диагонална матрица.

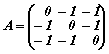
Решение:
Пресмятаме характеристичния полином на матрицата:

Намираме корените на характеристичния полином (напр. по правило на Хорнер):

Намиреме собствените вектори за λ1=1, като решения на системата (A-E)x=0:

Две линейно независими решения на тази система са a1=(1,-1,0) и a2=(1,0,-1) и всяко решение, т.е. всеки собствен вектор за собствена стойност 1, е от вида β.a1+γ.a2.
По метода на Грам-Шмид намираме  ортогонален базис на множеството от собствените вектори за собствена стойност 1:

Векторите b1 и b2 са ортогонални и собствени със собствена стойност 1.
Намиреме собствените вектори за λ3=-2, като решения на системата (A+2E)x=0:

Решение на тази система е a3=(1,1,1) и всички  собствени вектори със собствена стойност -2 са пропорционални на a3.
Векторите b1,b2,a3 образуват ортогонален базис на пространството защото b1и  b2 са ортогонални по построение, а a3 е перпендикулярен на b1 и b2 защото са собствени вектори с различни собствени стойности. Намерените вектори ги нормираме и получаваме следния ортонормиран базис на пространството:

Векторите от този базис са собствени  и затова матрицата на оператора в него е диагонална, като по диагонала стоят собствените стойности:

Задача 3 

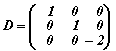Да се намери ортогонална матрица T и диагонална матрица D , такива че D=T-1AT , където

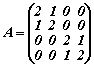
Решение:
Намираме характеристичния полином на матрицата:
Намираме характеристичните корени на матрицата: λ1=λ2=1 ,  λ3=λ4=3.
Решаваме системата (A-E)x=0:

Получените вектори c1 и c2 се оказоха ортогонални и затова няма нужда да прилагаме метода на Грам-Шмид за ортогонализация.
Решаваме системата (A-3E)x=0

Векторите c3 и c4 също са ортогонални, а решенията на едната система са ортогонални на решенията на другата система, защото са собствени вектори с различни собствени стойности на един симетричен оператор, който в стандартния базис има матрица A.
Нормираме получените вектори и така получаваме ортонормиран базис на четиримерното евклидово пространство. Записваме нормираните вектори като стълбове на матрица T. Тази матрица е ортогонална защото векторите образуват ортонормиран базис.

Ако матрицата A се разглежда като матрица на симетричен оператор в четиримерно евклидово пространство и ако направиме смяна на базиса към новополучения ортонормиран базис от собствени вектори, тогава матрицата на оператора в новия базис ще бъде диагонална и ще изпълнява търсената зависимост:  

Задача 4 (за самостоятелно решаване):
Спрямо ортонормиран базис e1,e2,e3  на тримерно Евклидово пространство E е зададен линеен оператор  φ по следния начин: 

Да се намери ортонормиран базис на пространството, в който оператора  има диагонална матрица, както и тази диагонална матрица.

Задача 5 (за самостоятелно решаване):
Спрямо даден ортонормиран базис  на тримерно линейно пространство  линеен оператор  φ има  матрица A. Да се намери ортонормиран базис на пространството, в който оператора  има диагонална матрица, както и тази диагонална матрица.

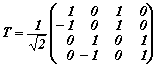Задача 6 (за самостоятелно решаване):

Да се намери ортогонална матрица T и диагонална матрица D , такива че D=T-1AT , където