симетричен оператор - свойства симетрични матрици собствени вектори канонизация

Собствени вектори на симетричен оператор

Тази страница е посветена на доказателството на съществуване на канонизация при симетричните оператори и тя включва:

	Теорема 1, в която се доказва, че симетричните матрици имат реални характеристични корени;
	Теорема 2: даваща че за симетричен оператор собствените вектори с различни собствени стойности са ортогонални;
	Теорема за съществуването на каноничен вид на симетричен оператор;
	Основни следствия от теоремата за канонизацията

Начина за прилагане на канонизацията е показан на следващата страница...

За да се намерят собствените вектори на един линеен оператор трябва първо да бъдат определени неговите собствени стойности, т.е. за матрицата на оператора в кой да е базис трябва да се определят характеристичните корени на матрицата и собствени стойности на оператора са тези характеристични корени на матрицата, които са реални числа. Доказахме Теорема, от която имаме, че в ортонормиран базис матрицата на симетричен оператор есиметрична и затова ще определим какви могат да са корените на симетрична матрица.

	Характеристиечен полином на една квадратна матрица A е		.
	Степента на характеристичния полином е равна на реда на матрицата и неговите корени се наричат характеристични корени на матрицата.

Известно е, че всеки полином с реални коефициенти има комплексни корени, но за реална симетрични матрици ще докажем, че всички характеристични корени са реални числа.

Теорема 1.

Характеристичните корени на симетрична матрица с реални елементи са реални числа.

Доказателството е изнесено на следната страница..

Един ненулев вектор g се нарича собствен вектор за линейния оператор φ, когато съществува число λ (което се нарича собствена стойност), такова че: φ(g)=λ.g .

Като следствие от теорема 1 непосредствено получаваме, че всеки симетричен оператор има собствени вектори.

Теорема 2.

Нека φ е симетричен оператор в евклидовото пространство E и векторите a и b са собствени вектори за различни собствени стойности. Тогава a и b са ортогонални.

Доказателство:
Нека		и		. Тогава е изпълнено		и следователно:

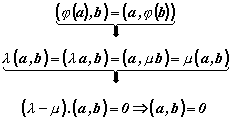За да докажем теоремата за канонизация на симетричен оператор, ще ни е нужна следната лема:

Лема:

Ако g е собствен вектор на симетричния оператор φ и h е вектор перпендикулярен на g тогава φ(h) също е перпендикулярен на g .

Доказателство:

Векторът g е собствен

φ(h)g)=λ.g . Тогава от (g,h)=0 имаме:

Теорема. ( канонизация на симетричен оператор):

За всеки симетричен оператор в крайномерно евклидово пространство съществува ортонормиран базис от собствени вектори на оператора.

Доказателство:

Доказателството се провежда по идукция онтосно n, размерността на пространството E

n=1=dimE и нека векторът e е единичен вектор от E. Този вектор сформира ортонормиран базис на пространството E и φ(e)=λ.

твърдението е вярно.

Нека твърдението е доказано за произволно (n-1) - мерно евклидово пространство и нека E е произволно n- мерно евклидово пространство.

Нека λ₁е реален характеристичен корен на матрицата на оператора (такъв съществува според Теорема 1) и нека a е собствен вектор, за който φ(a)=λ₁.a.

Нека бележим с U множеството от всички вектори на E, които са ортогонални на a, т.е. U={xE| (x,a)=0}.За U имаме:

	Uе подпространство на E с размерност *n-1* (пространството U е ортогонално допълнение на линейната обвивка на вектора a);
	В Лемата доказахме, че за всеки вектор x от U е изпълнено φ(x)U, следователно можем да резглеждаме φ също и като симетричен оператор действащ в пространството U .
	Съгласно индукционното предположение за U съществува ортонормиран базис e₁,...,e_n-1 от собствени вектори на оператора φ.

Нека e_n е единичен вектор получен чрез нормиране от a, тогава ясно е че векторите e₁,...,e_n образуват ортонормиран базис на E и всички те са собствени вектори за оператора φ. Следователно твърдението е вярно и за пространството E.

По индукция следва, че твърдението е вярно за произволно крайномерно евклидово пространство .

Следствие 1:

За всеки симетричен оператор съществува ортонормиран базис, спямо който матрицата на оператора е диагонална. (това е базиса от собствени вектори на оператора)

	Една квадратна матрица T се нарича ортогонална, когато нейната обратна съвпада с транспонираната и, T^-1=T^t.
	В Евклидово пространство матрицата на прехода от един ортонормиран базис към друг ортонормиран базис е ортогонална матрица.

Непосредствено от формулата за смяна на матрицата но оператор при смяна на базиса получаваме следното:

Следствие 2:

За всяка симетрична матрица A съществува ортогонална матрица T, и диагонална матрица D, такава че D=T^-1AT.