симетричен оператор - свойства симетрични матрици собствени вектори канонизация

Характеристични корени на симетрична матрица

В тази страница е изложено:

	подробното доказателство на теоремата, че всяка симетрична матрица с реални елементи има реални характеристични корени.
	Припомняне на основните свойства на комплексното спрягане при комплексни числа, защото тези свойства са от съществено значение при доказателството на теоремата.

Теорема:

Характеристичните корени на симетрична матрица с реални елементи са реални числа.

Доказателство:

Нека матрицата е A квадратна от ред n, тогава нейният характеристичен полином

е полином с реални коефициенти от степен n .

Нека λ₁е един корен на този полином и той в общия случай е комплексно число.Щом λ₁ е корен, следователно матрицата A-λ₁.E има детерминанта 0. Това означава,че хомогенната система с матрица A-λ₁.E има ненулево решение, но


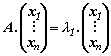следователно и системата		има ненулево решение.

Нека (α₁,...,α_n) е едно ненулево решение на тази система. Тъй като коефициентите на системата са комплексни числа, то и това решение в общия случай е комплексно.

Тогава е изпълнено

. Умножаваме отлява двете страни на това

равенството по вектора

и получаваме следното:

(1)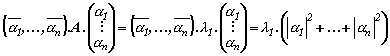

Транспонираме равенство (1) и получаваме

(2)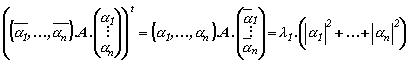

Вземаме комплексното спегнато на всички елементи от равенство (1) и получаваме:

(3)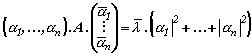

използвали сме, че матрицата A e с реални елементи и

Векторът (α₁,...,α_n) е ненулев и е изпълнено:

Левите страни на равенствата (2) и (3) съвпадат, следователно съвпадат и десните им страни:

Откъдето получихме, че характеристичния корен λ₁ е реално число и теоремата е доказана.

Да си припомним основните свойства на спрягането на комплексни числа, които бяха използвани в доказателството на горната теорема:

Комплексното спрегнато на

е числото

Основните свойства на комплексното спрягане са следните:





	λ е реално число тогава и само тогава когато .