за проекта за темата за автора  e-mail  

симетричен оператор - свойства симетрични матрици собствени вектори канонизация

Симетричен оператор - определение и основни свойства

В тази страница ще се запознаем с:
определение за симетричен оператор и основни примери;
свойството,че симетричните оператори образуват подпространство на пространството на всички линейни оператори
връзка между симетричен оператор в крайно-мерно пространство и симетрични матрици. Повече  свойства на симетричните матрици са дадени в страницата симетрични матрици.
Задачи за симетричен оператор- зад.1, зад.2,

Определение за симетричен оператор
Линейният оператор φ:E→E,  действащ в Евклидово пространство E, се нарича симетричен, ако за всеки два елемента x,yE e  изпълнено равенството:
Пример:   Във всяко Евклидово пространство нулевия и тъждествения оператор са тривиални  примери на симетричен оператор .                                                                                  

 

Свойство :
 Нека φ и ψ са симетрични оператори в евклидово пространство E, тогава φ+ψ  и
α.φ също са симетрични оператори за произволно реално число α.
Доказателство:

Това свойство ни задава, че множеството на всички симетрични оператори образува линейно подпространство на пространството от всички линейни оператори в едно Евклидово пространство.
Пример:  В едномерно Евклидово пространство всеки линеен оператор може да се получи чрез умножаване на число по тъждествения оператор и следователно всеки линеен оператор в едномерно пространство е симетричен.
 

Задача: 
В n-мерно Евклидово пространство E са дадени два единични и ортогонални вектори  a и b , т.е. |a|=1,  |b|=1 и (a,b)=0 и изображението φ:E→E,  което  е определено по следния  начин : φ(x)=(a,x).b+(b,x).a  за  произволен вектор xE. Да се  докаже, че φе симетричен оператор в E и че φ3=φ.
Решение.....  
 

Задача за упражнение: 
Нека φи ψ са симетрични оператори действащи в евклидово пространство E. Да се докаже, че  φ◦ψ+ψ◦φ е симетричен оператор.
 

Връзка между симетрични оператори и симетрични матрици

Теорема 1:

 Нека E  е крайномерно евклидово пространство и  φ е симетричен оператор в E. Тогава  φ има симетрична матрица  в кой да е ортонормиран базис на E .
Доказателство:
Нека   е един ортонормиран базис на E  , и нека φима
матрица  в този базис. .
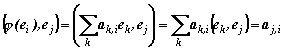и .
Тъй като φе симетричен, то  . Така получаваме, че  за 
произволни индекси  , т.е. A  е симетрична матрица.

 

   

Теорема 2

Нека E  е крайномерно Евклидово пространство и е ортонормиран базис  
в E . Ако един линеен оператор  има симетрична матрица в  , то
 оператора е симетричен.
Доказателство:
Нека и са два произволни вектори от E и
е матрицата на  в базиса , тогава:

Пресмятаме  и

A е симетрична матрица  откъдето получаваме че

 

Горните две теореми могат да се обединят в една по следния начен:
В крайномерно  Евклидово пространство един линеен оператор е симетричен, тогава и само тогава когато матрицата му в кой да е ортонормиран базис е симетрична.

 

Пример: Спрямо стандаретен ортонормиран базис на двумерното Евклидово пространство са дадени
векторите a=(1,1) и b=(1,2). Спрямо базиса a, b линейния оператор има матрица .
Виждаме, че . Аналогично
и операторът не е симетричен въпреки, че има симетрична матрица в един базис, който не е
ортонормиран.