Лекция 7
Тестове на Стюдент и Фишер
Тук ще дадем рецептите на няколко най-популярни статистичски
извода, базирани на разпределенията свързани с нормалното.
Ще разгледаме определени статистики, доверителни интервали за
нееизвестните параметри и хипотези свързани с тях
7.1 Доверителен интервал за дисперсия
Нека x О N(m,s2). Нека сме направили
n наблюдения. Намерете оптимална доверителна област за s2.
Статистиката S2 = еi = 1n(xi-m)2 има разпределение
s2c2n (определение 6.2).
От лема 3.2 следва, че доверителна област с минимална
дължина за S2 се дава от равенството:
|
P (ql Ј |
S2
s2
|
Ј qu) = 1-a. |
|
Тук квантилите на c2-разпределението ql,qu се определят
от уравненията
|
F(ql)+1-F(qu) = a, f(ql) = f(qu), |
|
където F и f са съответно функцията на
разпределение и плътността на c2-разпределение с
n степени на свобода. Окончателно получаваме:
Когато м.о. m е неизвестно, се използува
статистиката:
|
S2(x) = |
n
е
i = 1
|
(xi- |
_
x
|
)2, |
| (7.2) |
която не зависи от m и има разпределение
s2c2n-1. Останалото е същото.
Да отбележим, че на практика така определения интервал (с
минимална дължина) се използува рядко. По-често се приравняват
вероятностите на двете опашки: F(ql) = 1-F(qu) = a/2.
Така квантилите се вземат направо от таблицата.
7.2 Разпределение на Фишер
Определение 1
Разпределение на Фишер - Снедекор с r и s степени на свобода
има частното:
където c2r,c2s са независими сл.в. с c2
разпределение.
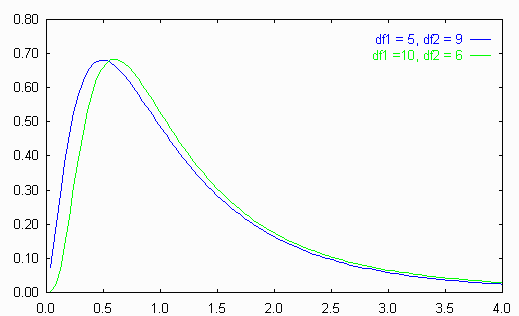
Фигура 7.1: Разпределение на Фишер - Снедекор
Теорема 1
Разпределението на Фишер Fr,s има плътност:
|
f(x,r,s) = C(r,s) xr/2-1 (1 + rx/s)-(r+s)/2, |
| (7.3) |
където x > 0 и C(r,s) - нормираща константа.
Докажете го. Можете да използувате направо определението. Иначе
може да използувате връзката между бета, гама и
F - разпределение:
7.2.1
Критерий на Фишер за независими извадки
Нека проверим хипотезата за равенство на дисперсии на две
различни генерални съвупности (г.с.) с нормално разпределение на
основата на независими извадки от тях с размери n1 и n2
съответно. Ще предположим, че средните на двете г.с. са
неизвестни. Да образуваме статистиките:
|
S2(x) = |
n1
е
i = 1
|
(xi- |
_
x
|
)2, S2(y) = |
n2
е
i = 1
|
(yi- |
_
y
|
)2. |
| (7.4) |
Съгласно определение 6.2 и теорема
6.4 (на Кокрън),
всяка от тези статистики има хи-квадрат разпределение,
умножено със съответната s2. Ако за нулева изберем
хипотезата: H0:s(x) = s(y), то
съгласно определение 7.1 частното:
|
f = |
S2(x)/(n1-1)
S2(y)/(n2-1)
|
= |
s2(x)
s2(y)
|
|
|
ще има разпределение на Фишер с (n1-1) и (n2-1)
степени на свобода съответно. Така с използуването на
тази статистика можем да проверяваме нулевата
хипотеза срещу различни алтернативи:
- За алтернативите H1:s(x) > s(y) (или
H1:s(x) < s(y)) критерият ще бъде равномерно най -
мощен.
Критичната област е W = { f > z}; F(z) = 1-a.
- За алтернативата H1:s(x) № s(y) не съществува
равномерно най - мощен критерий. На практика се използува следната
процедура. Извадката с по-малка извадъчна дисперсия s2 се
означава с y. Критичната област отново е
W = { f > z}; F(z) = 1-a. Така става възможно използуването
на таблици за квантилите само от горната половина на F
разпределението.
7.3 Разпределение на Стюдент
Определение 2
Разпределение на Стюдент T(n) с n степени на свобода има
частното:
където x,c2s са независими сл.в. с N(0,1) и c2(n)
разпределение с n степени на свобода съответно.
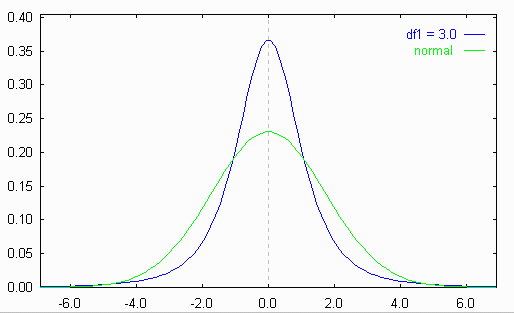
Фигура 7.2: Разпределение на Стюдент
Теорема 2
Плътността на разпределение на tn се задава с формулата
|
f(x,n) = Cn (1+ x2/n)-(n+1)/2 . |
| (7.5) |
Тук Cn е нормираща константа.
Докажете го. Може да се изведе направо. Може да се използува
връзката между T и F разпределения:
(tn)2 = f1,n.
От закона за големите числа следва, че граничното разпределение
на tn при n®Ґ е N(0,1).
7.3.1 Доверителен интервал за м.о. m
Нека x О N(m,s2). Нека сме направили
n наблюдения. Да намерим оптимална доверителна област за
m. Тук втория параметър s се смята за неизвестен.
Статистиката
има T-разпределение
с (n-1) степени на свобода и това разпределение не зависи
от s. Тук s2(x) = S2(x)/(n-1).
От лема 3.2 следва, че оптималната доверителна област за
[`(x)] е
Тук z се определя от уравнението F(z)-F(-z) = 1-a и се
нарича двустранен квантил на T-разпределение с n-1
степени на свобода за
критично ниво a. Така построения доверителен интервал
удовлетворява равенството: Fў(x) = Fў(-x), което следва
от симетричността на плътността (7.5) и, следователно,
е с минимална дължина.
7.3.2 Критерий на Стюдент
Нека пак предположим, че наблюденията са от N(m,s2).
Статистиката t (виж. 7.6) ще има T разпределение
независимо от s. Ако за нулева изберем хипотезата:
H0:m = 0, то това ни дава възможност да проверяваме нулевата
хипотеза срещу различни алтернативи:
- За алтернативата H1:m > 0 (или
H1:m < 0) критерият ще бъде равномерно най - мощен.
Критичната област е W = { t > z}; F(z) = 1-a.
- За алтернативата H1:m № 0 не съществува
равномерно най - мощен критерий.
Критичната област е W = {|t| > z}; F(z) = 1-a/2.
При голям брой на наблюденията (n > 100) разпределението на
Стюдент клони към стандартно нормално, така че се упростява
пресмятането на квантила.
7.3.3 Критерий на Стюдент за независими извадки
Нека са ни дадени независими извадки
x1,x2,...,xn и
y1,y2,...,ym от независими наблюдения, съответно, на
x1 О N(m1,s1) и
x2 О N(m2,s2). Задачата е по тези наблюдения да
проверим хипотезата, че двете генерални съвкупности съвпадат.
T.e. m1 = m2 и s1 = s2.
Отначало се прилага теста на Фишер за проверка на равенството
на двете дисперсии (виж.7.2.1). Разпределението на Фишер
не зависи от стойностите на неизвестните м.о. на двете
популации.
При отхвърляне на нулевата хипотеза H0: s1 = s2
задачата е решена - двете популации се приемат за различни. Ако
обаче нямаме основания да я отхвърлим, преминаваме към проверката
за равенство на м.о.
Да разгледаме хипотезата H0:m1 = m2 срещу алтернативата
H0:m1 № m2 при условие, че s1 = s2 = s.
Да разгледаме обединената
(виж.7.4)
оценка на дисперсията s2:
|
s2 = |
1
n+m-2
|
(S2(x)+S2(y)) |
| (7.7) |
Тя е неизместена и разпределението на (n+m-2)s2/s2 е
очевидно c2n+m-2. От друга страна сл.в.
|
|
_
x
|
- |
_
y
|
О N(m1-m2,s2( |
1
n
|
+ |
1
m
|
)). |
|
Двете сл.в. са независими и, следователно, при изпълнена
H0:m1 = m2 статистиката:
ще има разпределение Tn+m-2. Това ни дава възможност, както и
по-горе да си проверяваме нулевата хипотеза при различни
алтернативи. Така на втората стъпка окончателно ще можем да
отговорим за равенството на двете популации.
Със същия критерий може да се проверява и равенство само на
м.о. на две г.с. Но формулите за пресмятане на съответната
статистика се различават, когато не приемаме за равни дисперсиите
им.
File translated from TEX by TTH, version 2.10.
On 5 Apr 1999, 17:47.


