Тази лекция съдържа факти от теория на вероятностите, необходими за строгото обосноваване на многомерните статистически процедури. Резултатите ще бъдат изложени тук като следствия от свойствата на нормалното разпределение.
Сведенията от тази лекция могат да бъдат намерени без особени затруднения във всяка книга по математическа статистика или теория на вероятностите.
Определение 1
Плътността на стандартното нормално разпределение
в Rn има вида:
f(x) =
1
(2p)n/2
e-||x||2/2, (6.1)

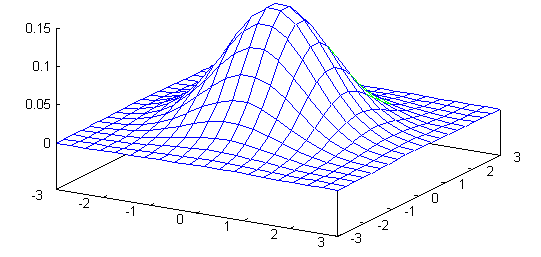
От определението се вижда, че тази плътност зависи само от нормата на вектора x и, следователно, е инвариантна относно всякакви ортогонални трансформации - те запазват нормата и имат якобиян равен на 1. Също така е ясно, че тя може да се представи като произведение на n едномерни стандартни нормални плътности (виж фиг.6.1).
До края на тази лекция ще предполагаме, че случайната величина x има стандартно нормално разпределение в Rn. Плътността на многомерното нормално разпределение от по - общ вид N(m,C) в Rn има вида:
| (6.2) |
И тук както в едномерния случай имаме връзка между параметрите на закона и моментите на сл.в.:
Теорема 1
Ако h О N(m,C), то
E h = m, E (h-m)(h-m)ў = C .
Теоремата може да се докаже с проста смяна на променливите или като следствие на следната по - обща теорема.
Теорема 2 Случайната величина h = Tx+ a, където T е неизроден линеен оператор от Rn в Rk (n і k), има разпределение N(a, TTў) в Rk.
От тази теорема следва, че всички маргинални разпределения (или проекции в произволна размерност) са нормални. Следва също, че произволна линейна функция от (зависими или независисми) нормални сл.в. е нормална сл.в.
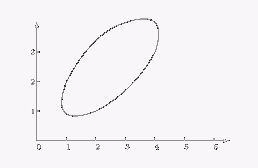
Верно е също, че и условните разпределения (при линейни ограничения от типа на равенството) са гаусови.
Доказателство: Ще разгледаме само случая h = Tx. В случая операторът T се представя просто като матрица с k Ј n реда и n колони и трябва да притежава пълен ранг k. Това означава, че нейните редове са линейно независими вектори в Rn. Нека означим с S подпространството от линейните им комбинации. То очевидно има размерност k. Нека допълним редовете на T с n-k ортогонални помежду си и на S единични вектори и означим така получената матрица с [(T)\tilde]. Тогава по формулата за смяна на променливите [(h)\tilde] = [(T)\tilde]x ще има разпределение с плътност:
|
| ||||||||
Определение 2 Случайната величина c2n = xўx има разпределение c2(n) с n степени на свобода.
Теорема 3
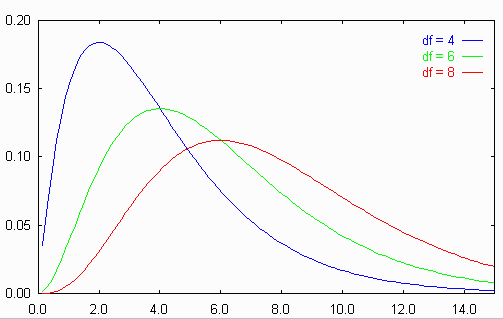
Случайната величина c2n има плътност:
f(x,n) = C(n) xn/2-1 e[(-x)/ 2]. (6.3)
Веднага се вижда, че това е гама-разпределение G(n/2,1/2) и изводът може да се направи по индукция от n = 1 и възпроизводящите свойства на гама-разпределението: G(a,l)+G(b,l) = G(a+b,l).
Средната стойност на c2n = xўx е очевидно n, а дисперсията лесно се пресмята и е равна на 2n. От следната проста лема непосредствено се вижда, че разпределението c2n = xўx не може да се получи от друга квадратична форма на n гаусови сл.в., освен тривиалната.
Лема 1 Нека xi,i = 1,...,n са независими сл.в. с еднаква дисперсия и li,i = 1,...,n са такива, че еi = 1nli = 1. Тогава сл.в. h = еi = 1nlixi има минимална дисперсия, когато li = 1/n,i = 1,2,...,n.
Доказателство: Да предположим, че D(xi) = 1. Тогава D(h) = еi = 1nli2. В сила е обаче неравенството:
|
Лема 2 Ако дадена квадратична форма Q има ранг q и сл.в. xўQx има разпределение е c2q, то Q е проектор.
Доказателство: Да напомним, че проекторите са неотрицателно - определени оператори (т.е. са самоспрегнати Pў = P), а освен това са и иденпотенти (P2 = P ). Това значи, че собствените им числа могат да бъдат само 0 или 1. Естествено, броят на ненулевите собствени числа е равен на ранга.
За доказателството е достатъчно да сравним дисперсиите на двете разпределения и да се възползуваме от лема 6.1. Ние обаче ше го изведем директно - така ще пресметнем и дисперсията на c2q разпределение.
Действително, Q е неотрицателно определена и значи може да се представи като Q = UDUў, където U е ортогонална матрица, а D - диагонална. Тогава сл.в. xўQx и xўDx имат едно и също c2(q) разпределение.
|
Теорема 4 Теорема на Кокрън. Нека Q,R,S са неотрицателно определени матрици с рангове q,r,s съответно, Q = R + S и случайната величина xўQx има разпределение c2(q). Случайните величини xўR x и xўS x са независими и имат разпределения c2(r) и c2(s) тогава и само тогава, когато q = r+s.
Доказателство: Първо да отбележим, че съгласно лема 6.2 матрицата Q е проектор и можем да се ограничим в пространство с размерност q, когато Q = I.
Достатъчност. Имаме: I = R+S = U(DR+DS)Uў. Следователно, I = DR+DS. Ако q = r+s, то DR и DS имат съотвения брой ненулеви елементи, значи R и S са проектори и RS = SR = 0. За доказателството на независимостта използуваме равенството: ||Qx||2 = ||x||2 = ||Rx||2 +||Sx||2 за всяко x и xўRўRx = ||Rx||2 = xўRx. Остава да приложим теорема 6.2 за операторите R и S и определението на хи-квадрат разпределение.
Необходимост. Равенството q = r+s следва директно от лема 6.2. Q.E.D.
Частен случай от теоремата на Кокрън е независимостта на [`(x)] = 1/nеxi и S2 = е(xi-[`(x)])2. Наистина,
|
| |||||||||||||||||||||||||||||||
Пример 1 Условно математическо очакване и коефициент на корелация.
Нека случайната величина x О R2 и има разпределение N(m,S). Тогава условното математическо очакване и коефициентът на корелация се получават по формулите: E (x2|x1) = a x1 + b, r(x1,x2) = a /S22, където b = m2 - a m1, a = S12 (S22/S11)1/2. С Sij сме означили елементите на ковариационната матрица на двумерната сл.в. x. В частност S22 = s2(x2).
Проверете тези формули.