В тази лекция ще се спрем само на модели за проста независима извадка, когато наблюденията се интерпретират като независими сл.в. с еднакво разпределение. В статистиката обикновено се предполага, че това разпределение е неизвестно.
Когато разпределението е неизвестно с точност до определянето на някои параметри, методите на статистиката се наричат параметрични. В противен случай те са непараметрични.
Ще си поставим следните цели:
Статистическите изводи са заключения за различни свойства на генералната съвкупност направени въз основа на наблюденията и различни предположения за генералната съвкупност. Така ако предположенията са верни, нашите твърдения стават функции на извадката, т.е. придобиват случаен характер - стават сл. в. Тъй като твърденията примат две ''стойности'' - истина и неистина, задачата всъщност е да намерим вероятността едно заключение да бъде верно.
Най-популярната и коректна форма за построяване на статистически извод е статистическата хипотеза. Много често имаме основания да предположим за неизвестното разпределение на генералната съвкупност, че то притежава плътност f(x). Така е и по - лесно да построим ''оптимална'' критична област. За основен инструмент ни служи следната знаменита лема.
Лема 1
( Нейман-Пирсън)
Нека са дадени две плътности f0(x), f1(x). Тогава решението на
разпределителната задача:
sup
W
у
х
W
f1(x) dx при фиксирано a =
у
х
W
f0(x) dx (3.1)
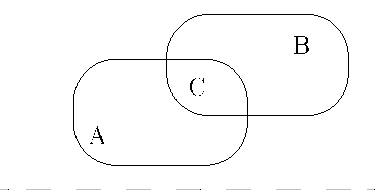
Доказателство: Нека W = {x:f1(x) і c f0(x)} и a = тW f0(x) dx . Нека Wў е такова, че a = тWў f0(x) dx . Да разгледаме разликата:
| |||||||||||||||||||||||||||||||||||||

Тук сме означили A = W\Wў,B = Wў\W,C = W Wў или W = A+C,Wў = B+C, както това е показано на фигурата.Q.E.D.
Резултатът се използува по следния начин. Искаме да проверим хипотезата H0 , че наблюдението има плътност f0(x) срещу контра хипотезата или алтернативата H1, че то има плътност f1(x). Решението, което ше вземем съответно е, че хипотезата ни H0 е вярна или не. Когато наблюдението попадне в критичната област W отхвърляме хипотезата и обратно, когато попадне извън нея, я приемаме. Естетвено си задаваме критичното ниво a = тW f0(x) dx , което всъщност представлява вероятността да отхвърлим вярна хипотеза, като малко число - например 0.05.
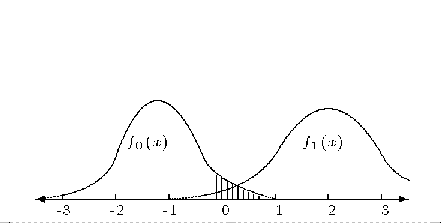
Числото a наричаме грешка от първи род, а числото 1-a - ниво на доверие. На фиг. 3.2 защрихованата площ под кривата е равна на a. Тук алтернативата f1 е отдясно на основното разпределение и критичната област е съответно в дясната част на основното разпределение f0. Естествено, ако f1 беше отляво, критичната област щеше да бъде наляво.
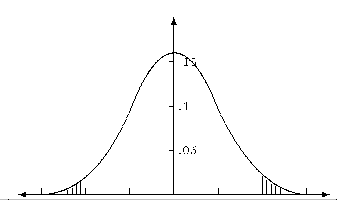
Когато алтернативата е със значително по - голяма дисперсия, съгласно лемата на Нейман - Пирсън ще получим двустранна критична област. Същата област ще се получи и, когато ''нямаме алтернатива''.
Възможна е и обратната грешка b- грешка от втори род - да приемем хипотезата, когато тя не е вярна. Естествено е нашето желание да търсим критичната си област така, че запазвайки a да минимизираме b. Лемата на Нейман - Пирсън ни дава средство лесно да строим оптимални критични области. Тя може да се използува и за произволни функции от наблюденията. Числото 1-b се нарича мощност на критерия (критичната област) и е различно за всяка конкретна алтернатива.
Пример 1 Нека H0: x О N(0,1), а H1: x О N(1,1). Нека сме направили n наблюдения. Намерете оптималната критична област.
Решение. Векторното наблюдение x ще има за плътности и при двете хипотези многомерната нормална плътност с единична ковариационн матрица, но различни средни стойности. От лемата 3.1 следва, че оптималната критична област има вида:
| |||||||||||||||||||
Пример 2 Нека H0: x О N(0,1), а H1: x О N(0,s2), s > 1 - неизвестен параметър. Нека сме направили n наблюдения. Намерете оптималния критерий за всяка от тези алтернативи.
Когато нямаме възможност да изберем разумна проста алтернатива построяването на критерий (критична област) с максимална мощност е затруднително. В някои случаи, обаче, това става лесно. В пример 3.1 се вижда, че за всички алтернативи (със средна стойност по - висока от 0) решението ще бъде същото.
Определение 1 Казваме, че критерият е равномерно най-мощен за дадено множество алтернативи, ако той е оптимален за всяка алтернатива поотделно.
Така на фигура 3.2 е показан критерий, който е равномерно най - мощен за всички ''десни'' алтернативи.
Пример 3 Нека H0: x О N(0,1), а H1: x О N(q,1), q - неизвестен параметър с произволен знак. Нека сме направили n наблюдения. Не съществува равномерно най - мощен критерий за това множество алтернативи.
Докажете го.
Тогава възниква необходимостта да направим статистически изводи за този параметър. Едно естествено заключение за числов параметър би било твърдение за принадлежността на неизвестния параметър към някоя област. Наричаме такава област доверителна, а вероятността на твърдението доверителна. Ясно е, че колкото по - широка е областта, толкова по - вероятно е неизвестния параметър да попадне в него. Естествено би било да поискаме и тук някаква оптималност - например, областта да има минимален обем при фиксирана вероятност. Когато говорим за едномерен параметър, се интересуваме от доверителни интервали с минимална дължина.
В такава постановка задачата много прилича на лемата на Нейман - Пирсън. Първоначално ще построим доверителна област за наблюдението, така че тя да има минимален обем. В последствие (при подходящи условия) тя ще се превърне в доверителна област за параметъра.
Лема 2
Нека е дадено семейството плътности f(x,q). Тогава
решението на разпределителната задача:
inf
U
у
х
U
dx при фиксирано a =
у
х
U
f(x,q) dx (3.2)
Доказателство: Абсолютно същото като на оригиналната лема.Q.E.D.
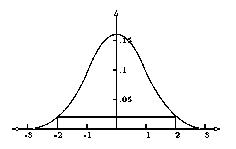
Нека сега решаваме задачата в случая, когато f(x,q) = f(x-q) - т.е. разпределението е известно с точност до неизвестен параметър на локация. От лемата следва, че в едномерния случай, когато имаме унимодално разпределение, трябва да построим доверителния интервал така, че плътността да бъде равна в двата края. Обикновено това е достатъчно за проверка на оптималността (минималната дължина) на така построения доверителен интервал.
Пример 4 Нека x О N(q,1). Нека сме направили n наблюдения. Намерете оптимална доверителна област за q.
Решение 1. Векторното наблюдение x ще има за плътности многомерната нормална плътност cn e-1/2||x-qe||2 . От лемата 3.2 следва, че оптималната доверителна област за x има вида:
|
Сега нека разгледаме внимателно това решение. Имаме равенството:
|
Така във всички разгледани до сега примери ние стигнахме до изучаването на статистики, които са свързани с определени параметри на разпределението в генералната съвкупност. Като сл.в. те притежават разпределение и при правилни предположения могат да се смятат някои характеристики на тези разпределения. Тъй като в момента говорим за неизвестни параметри, естествено е да наречем статистиките оценки . За да избегнем безмислената оценка q, ще разглеждаме като оценки на неизвестния параметър само такива функции на наблюденията, в аналитичния израз на които не участвува този неизвестен параметър.
Ще се върнем отново към пример 3.4.
Решение 2. Статистиката [`(x)] има разпределение N(q,1/n). Доверителна област за [`(x)] може да бъде
|
Двете решения, които предложихме, са очевидно различни. Кое от тях е по - добро и как да търсим възможно най - добрите оценки и строим най - правдоподобни твърдения ни учи т.н. теория на оценявяне на параметри, която ще разгледаме в следващите лекции.