Предишна тема Съдържание Следваща тема

Тема 15   Процеси с независими нараствания

15.1   Въведение

Нека разгледаме семейството от случайни величини {xt, t і 0}. За нас параметърът t ще има ролята на време и затова такива семейства ще наричаме случаен процес. Процесите с дискретно време всъщност представляват редици случайни величини. Теория на случайните процеси представлява специален раздел в теория на вероятностите с голямо значение. (виж. [(Гихман и Скороход,1977)])

За всяко t е определена функцията на разпределение F(x, t) = P(xt < x) и моментите на процеса (когато те съществуват) m(t)= E  xt, s2(t)= E  (xt-m(t))2 и т.н. Ще предположим, че сл.в. x0 = 0 и семейството F(x, t) е непрекъснато в нулата, т.е. F(x, +0) = F(x, 0) . Нека означим с qt1, t2 = xt2-xt1 нарастванията на процеса.

Определение 15.1   При тези предположения ще казваме че процесът е с независими нараствания, ако сл.в. qt1, t2 и xt2 са независими за всички t1, t2.
Това определение не е най-точното, но за нашите цели е напълно достатъчно. Всъщност би трябвало да поискаме независимост в съвкупност на всеки краен брой нараствания.

Определение 15.2   Процес с независими нараствания ще наричаме еднороден (е.п.н.н.), ако разпределението на сл.в. qt1, t2 зависи само от разликата на двата параметъра t2-t1.

От това определение е ясно, че за е.п.н.н. сл.в. qt1, t2 и xt2-t1 имат еднакво разпределение. Също така от тук следва, че моментите на процеса (когато съществуват) удовлетворяват съотношенията: m(t1+t2)=m(t1)+m(t2), s2(t1+t2)=s2(t1)+s2(t2).

15.2   Характеристична функция

Нека разгледаме сега семейството от характеристични функции определени от еднороден процес с независими нараствания.

f(t, t )= E e
itx
 
t
 
= у
х
Ґ


-Ґ
eitx d F(x, t)     (15.1)

Първо ще докажем една проста лема.

Лема 15.1   Ако комплексната функция от реален аргумент удовлетворява условията: F(0)=1, непрекъснатост в нулата и функционалното уравнение: F(x1+x2)=F(x1) F(x2) за всички реални x1, x2, то:
а. F(1) № 0;
б. F(x) = F(1)x.

Доказателство: а. Допускаме противното. Тогава от равенството 0=F(1)=F(1/n)n следва 0=F(1 /n) за всяко n, което противоречи на непрекъснатостта в нулата.

б. За рационални x= m / n имаме F(x) = F(1)x. Но от непрекъснатостта в нулата следва непрекъснатост за всяко x:
F(x+D x) = F(x)F(D x)   F(x).
Следствие Ако реална функция от реален аргумент удовлетворява условията: F(0)=0, непрекъснатост в нулата и функционалното уравнение: F(x1+x2)=F(x1)+F(x2) за всички реални x1, x2, то F(x) = F(1) x.



Доказателство: Достатъчно е да разгледаме функцията eF(x) и приложим лемата.

Теорема 15.1   За всеки еднороден процес с независими нараствания е изпълнена следната формула представяне на характеристичните му функции:
ln f(t, t ) = t
 
lim
Dt   0
1
Dt
у
х
Ґ


-Ґ
(eitx-1)d F(x, Dt)     (15.2)

Доказателство: Нека фиксираме t. Тогава f(t, 0)=1, функцията f е непрекъсната по втория си аргумент в нулата (от условието за непрекъснатост на семейството от функции на разпределение ) и удовлетворява функционалното уравнение. Прилагаме лемата и получаваме:
f(t, t) = (f(t, 1))
t
 
= e
t ln f(t, 1)
 

Тъй като логаритъмът е многозначна функция, при логаритмуването получаваме:
ln f(t, 1) = ln | f(t, 1)| + i(arg f(t, 1)+ 2kp).

Но f(t, 1) № 0 и можем да изберем k така, че f(0, 1)=1 - само тогава f(., 1) е характеристична функция.

Да разгледаме сега диференчното частно (t - фиксирано):
f(t, Dt)-1
Dt
=
e
Dt ln f(t, 1)
 
-1
Dt
= ln f(t, 1) + 0(Dt)=
1
t
ln f(t, t)+0(Dt).

Тук функцията 0(Dt) клони към нула, когато Dt клони към нула.

От друга страна, същото частно може да се запише така
f(t, Dt)-1
Dt
=
1
Dt
у
х
Ґ


-Ґ
(eitx-1)d F(x, Dt).

15.3   Поасонов процес

Тук като един от примерите за е.п.н.н. ще разгледаме процес с дискретно пространство на състоянията.
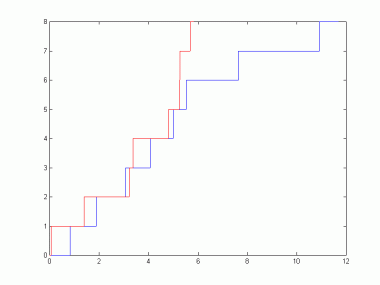Тук сме показали две траектории на такъв процес. Изискването случайните величини да приемат за стойности само натуралните числа и свойството за независимост на нарастванията автоматически налага такава форма на траекториите.
Фигура 15.1: Поасонов процес

Да означим съответните вероятности с Pk(t)= P (xt=k), k= 0, 1, 2, .... Ясно е, че от непрекъснатостта на семейството от функции на разпределение следва, че Pk(t)   0, когато t   0 за всяко k № 0 и P0(t)   1.



Теорема 15.2   Нека допълнително поискаме условието ( условие за ординарност)

 
S
k і 2
Pk(t) = o(P1(t)).     (15.3)
Тогава
F(x, t)=
 
S
k < x
(lt)k
k !
e
-lt
 
,
т.е. всички разпределения са Поасонови.
Тук o(e) означава произволна функция такава, че o(e)/e   0, когато e   0.

Доказателство: Ясно е, че P0(0)=1, P0(t1+t2)=P0(t1) P0(t2) и P0(.) е непрекъсната в 0. Тогава от лемата следва, че може да запишем P0(.) във формата P0(t)=P0(1)t=e-lt. Тук P0(1)=e-l, l > 0. Тогава P1(t) Ј Sk і 1 Pk(t) = 1 - e-lt   0.

За да изразим останалите вероятности, вече ще трябва да използуваме условието за ординарност. Имаме, че за всяко t е изпълнено равенството:
P0(t)+P1(t)+
Ґ
S
k=2
Pk(t)=1.
Следователно
P0(Dt)=e
-lDt
 
= 1-lDt+o(Dt)
P1(lDt)=lDt+ o(Dt)
Ґ
S
k=2
Pk(Dt)=o(Dt),

Сега използуваме представянето на характеристичната функция на е.п.н.н.:
ln f(t, t)= t
 
lim
Dt   0
1
Dt
у
х
Ґ


-Ґ
(eitx-1)d F(x, Dt)=
t
 
lim
Dt   0
1
Dt
( (e-it0-1) P0(Dt)+ (e-it1-1) (lDt+o(Dt))+ o(Dt))=
= t l (e-it-1).
Следователно получаваме
f(t, t)=e
t l (e-it-1)
 
,     (15.4)
което е характеристичната функция на Поасоново разпределение.

Пример 15.1   В телефонна станция постъпват средно по 60 повиквания за един час. Каква е вероятността да не постъпи нито едно повикване за 30 сек.
Решение: P (x1/2=0)= e- l/2=e-1/2=0.6065.

Пример 15.2   Колко стафидки трябва да сложим в тестото, така че с вероятност .99 във всяка кифличка да попадне поне една стафидка.
Решение: Да означим с l броят стафиди на единица обем и с v обема на една кифличка. Имаме
P  (xv і 1)= 1 - e
- l v
 
і .99
e
-l v
 
< 0.01, l v > ln 100 = 4.6
Следва да предвидим в тестото по 4.6 стафидки на кифличка.

15.4   Винеров процес

Ще разгледаме втори пример за е.п.н.н. Този път на случайните величини ще бъде разрешено да приемат произволни реални стойности.За сметка на това ще наложим ограничение върху съществуването и ''пренебрежимостта'' на третия момент:
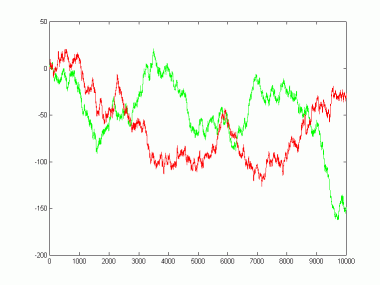у
х
Ґ


-Ґ
|x|3d F(x, Dt) = o(Dt)     (15.5)
Тук са нарисувани две симулирани траектории на стандартно Брауново движение. Те апроксимират при подходяща нормировка траекториите на стандартен Винеров процес.
Фигура 15.2: Винеров процес

Теорема 15.3   При указаните изисквания характеристичните функции на процеса имат представянето

ln f(t, t)= itmt -
1
2
s2 t2t ,
където m и s >0 са подходящо подбрани константи.
Така всички разпределения на процеса стават гаусови. Когато m=0 и s=1 процесът се нарича стандартен Винеров процес или Брауново движение с непрекъснато време.



Доказателство: Да отбележим, че съществуването и непрекъснатостта в нулата на третия абсолютен момент влече съществуването и непрекъснатостта на първия и втория моменти в нулата.

m(t) = у
х
Ґ


-Ґ
xd F(x, t),     s2(t)= у
х
Ґ


-Ґ
x2d F(x, Dt) - m2(t)

Да разгледаме функцията m(t). Имаме m(0)=0, m(t1+t2)=m(t1) + m(t2) и непрекъснатост в нулата. От следствието на лемата следва, че съществува константа m такава, че m(t)=m t. Същото е верно и за функцията s2(t)=s2 t.

Нека приложим сега нашата теорема за е.п.н.н.
ln f(t, t)= t
 
lim
Dt   0
1
Dt
у
х
Ґ


-Ґ
(eitx-1)d F(x, Dt)=
t
 
lim
Dt   0
1
Dt
( у
х
Ґ


-Ґ
(eitx-1-itx+
t2x2
2
)d F(x, Dt)+
+itmDt -
t2
2
(s2 Dt + m2 Dt2) ).
Първият член на това представяне клони към нула поради неравенството |eitx-1-itx+t2x2/2| Ј |t3x3|/6. Последният член е квадратичен по Dt и също клони към нула. Останалите два члена са търсените.



15.5   Гранична теорема

Ергодично свойство ще наричаме преход в някакво състояние на случайния процес независимо от началното състояние. Тук ще докажем една проста теорема за еднородните процеси с независими нараствания и крайна дисперсия - аналог на централната гранична теорема.

Да означим нормирания и центриран случаен процес с ht=xt-mt/st и с F(x) ф.р. на стандартното гаусово разпределение.

Теорема 15.4   На лице е сходимостта:
 
lim
t   Ґ
F
 
h
(x, t)= F(x).

Доказателство: Характеристичната функция на модифицирания процес е:
ln f
 
h
(t, t)=ln (
e
i
tm
s t1/2
 
f(
t
s t1/2
, 1)
t
 
)= i
t m
s t1/2
+t ln f(
t
s t1/2
, 1) ,
където mt=m t и st2=s2 t. Нека сега развием характеристичната функция ln f(t, 1) в ред на Тейлор около нулата (ln f(0, 1))'= f'(0, 1) = im и (ln f(0, 1))'= f'(0, 1) = - (s2 + m2):
ln f(
t
s t1/2
, 1) = im
t
s t1/2
- (s2 + m2)
t2
s2 t
+o(
1
t
).
Остава да извършим умножението и съкратим излишните членове.

15.6   Заключителни бележки

И двата примера изложени в предходните секции се оказа, че притежават крайни дисперсии и даже моменти от произволен ред. Това се дължи на наложените ограничения, които водят до диференцируемост на характеристичните функции по първия аргумент. За съжаление това не винаги е така, както показва следният пример:
ln f(t, t)= a t |t|
g
 
.
При g = 1 такава характеристична функция съответствува на разпределение на Коши, което не притежава даже първи момент.Проверете, че такова семейство характеристични функции може да бъде получено чрез теоремата и напишете в този случай съответното твърдение.
Д.Въндев -Теория на вероятностите - January 9, 2002
Предишна тема Съдържание Следваща тема