


Тема 16 Марковски вериги
Марковските процеси са обобщение на процесите с независими нараствания. Нека е
зададен процесът xt, t і 0.
Определение 16.1
Ще казваме, че процесът е Марковски, ако бъдещето и миналото
са независими при фиксирано настояще.
Същият смисъл имат думите: Бъдещето зависи само (се определя
изцяло) от последния наблюдаван момент. Разгледания в миналата
лекция Поасонов процес е очевиден пример за Марковски процес.
Състоянието на процеса в даден бъдещ момент е проста сума на
състоянието му в момента и съответната случайна величина
определяща нарастването му. Така е очевидно и за всички процеси с
независими нараствания --- те са марковски.
За разлика от е.п.н.н., Марковските процеси могат да
притежават и стойности, които не са числови. Наистина,
стойностите на е.п.н.н. трябва да принадлежат на
адитивна група --- това изисква определението им.
Особеността при дефиниция на марковски процеси идва от това,
че трябва да се разглежда и проверява условна независимост.
Когато вероятността на дадено фиксирано състояние е нулева (както
това е при процеси с непрекъснато пространство на състоянията),
такава проверка е нетривиална --- тя изисква наличието на
многомерна вероятностна плътност.
16.1 Марковски вериги
Тук ще се спрем на процеси с дискретно време и крайно
дискретно пространство на състоянията. Такива процеси наричаме
марковски вериги. Подробно с тях може да се запознаете в книгите
[(Кемени и Снелл,1970)] и [(Димитров,1980)]. Ще предположим, че множеството
от състояния на веригата са числата 1,2,...,k.
Ако условно означим събитията в ''миналото'', ''настоящето'' и
''бъдещето'' със буквите A, B, C, то Марковското свойство
означава просто P (AЗ C|B)=P (A|B)P (C|B).
Сега дефиницията за марковост може да се препише по - точно:
Определение 16.2
Ще казваме, че процесът е крайна Марковска верига, ако за всички
възможни набори {i0,i1,... ,in}, (1Ј ikЈ k) и всяко nі 1 е
изпълнено:
P (x0=i0,x1=i1,... ,xn=in,xn+1=in+1|xk=ik)=
P (x0=i0,x1=i1,... ,xk-1=ik-1|xk=ik)*
P (xk+1=ik+1,... ,xn=in|xk=ik).
Марковското свойство дава възможност съвместните разпределения на
множеството случайни величини да бъдат пресмятани просто,
както показва следната теорема.
Теорема 16.1
Разпределенията на крайна Марковска верига се определят от
началното разпределение {pi=P(x0=i),i=1,2,... ,k} и
матриците на преходни вероятности (във всеки един момент
{n=0,1,2,...} на времето)
Pi,j(n)=
P (xn+1=j|xn=i), (i,j=1,2,... k,) по
формулата:
|
P |
(x0=i0,x1=i1,... ,xn=in) = p |
|
P |
|
(0)... P |
|
(n-1).
(16.1) |
Доказателство: Доказателството се прави по индукция и следва лесно от
определението и формулата за умножение на вероятности. Да отбележим, че
понеже P (A|B)=P (AЗ B|B),
Марковското свойство може да се запише и така:
P (AЗ BЗ C|B)=P (AЗ B|B)P (CЗ B|B).
Нека да допуснем, че сме доказали формулата
(16.1) за някое n (за n=0,1 тя е очевидна) и всички
възможни набори {i0,i1,... ,in}. От определението
16.2 следва формулата:
| P (AЗ BЗ C|B)=
P (x0=i0,x1=i1,... ,xn=in,xn+1=in+1|xn=in)= |
| P (x0=i0,x1=i1,... ,xn=in|xn=in)
P (xn=in,xn+1=in+1|xn=in)= |
| P |
(x0=i0,x1=i1,... ,xn=in|xn=in)P |
|
(n)
=P (AЗ B|B)P (C|B) |
|
Като умножим тази формула с вероятността P (B)=P (xn=in) получаваме
търсената рекурсия.

Определение 16.3
Ще казваме, че Марковската верига е еднородна, ако преходните вероятности
Pi,j(n) не зависят от n.
Да означим тази единствена матрица на преходните
вероятности с P и вектора от началните вероятности с p0.
Матрицата P се нарича стохастична, защото сумата на елементите й
по редове е 1. Една от основните задачи на теорията на Марковските
вериги е изследването на граничното поведение на Pn=P*P*··· *P. Да
означим елементите на тази матрица с pi,jn, n=2,3,... .
Очевидни са следните уравнения на А.Марков:
|
|
pi,jn+1 = |
|
pi,l pl,jn
(16.2) |
Сега лесно можем да изразим и вектора от вероятности в момента n:
pn={P (xn=i)}, (i=1,2,... ,k):
p'n = p0'Pn .
16.2 Гранично и стационарно разпределения
Следната теорема се нарича ергодична теорема на А.А.Марков
Теорема 16.2
Ако всички елементи на стохастичната матрица са строго положителни, то
съществуват числа pj, 0 Ј pj Ј 1, Sj pj= 1, такива че
limn  Ґ pi,jn =pj независимо от индекса i.
Ґ pi,jn =pj независимо от индекса i.
Доказателство: Снабдяваме линейното пространство Rk с норма:
||x||=Si=1k |xi|. В тази норма то е пълно --- всяка
сходяща по Коши редица има граница. Да разгледаме подмножеството
K на Rk определено от условията: Si=1k xi = 1, xi
і 0, i=1,2,... ,k.То е компактно и трансформацията P го
изобразява в себе си. Ще покажем, че P е свиваща трансформация
и, следователно, има единствена неподвижна точка, към която се
стремят неговите итерации.
А. Върху елементите на K разстоянието, породено от указаната
норма, се пресмята по следния начин:
|
||x-y||= 2 |
|
(xi - yi).
(16.3) |
Б. Нека означим с a = mini,jpi,j. Тогава е
изпълнено условието за свиване:
||
x'
P-
y'
P||
Ј (1-
a)||
x -
y||.
(16.4)
| ||x'P-y'P||= |
|
= |
| = |
|
Ј |
| Ј |
|
Ј |
| Ј |
|
= (1-a)||x -y||. |
В. Нека означим със z неподвижната точка на P -
точката, удовлетворяваща уравнението: z'P=z'.
Тъй като диаметърът на множеството K е 2 имаме:
||z' - x'Pn||Ј ||(z-x)'Pn||Ј 2 (1-a)n.
Г. Тогава границата PҐ съществува, тя
е линеен оператор и е проектор върху тази точка и, следователно,
може да се запише във формата: PҐ= e z'.

Коментар
От доказателството е ясно, че граничното състояние на такава
верига е единствено и се достига с експоненциална скорост.
Ясно е също, че теоремата може да се приложи и за вериги, при
които само някаква степен на преходната матрица притежава
положителни членове.
Определение 16.4
Ще наричаме разпределението
p={pi, i=1,2,... ,k} върху
пространството на състояния на еднородна крайна Марковска верига
стационарно, ако удовлетворява следното съотношение:
Теорема 16.3
Граничното разпределение (когато съществува) е стационарно.
Доказателство: Удобно е да се използуват за целта т.н. уравнения на
Колмогоров:
Те се извеждат точно както и уравненията на Марков
(16.2). Не е трудно да се провери за граничното
разпределение, че то трябва да ги
удовлетворява, т.е. да бъде стационарно.
Да означим вектора e={1,1,...,1}' и с p - този от
граничните вероятности. Тогава от съществуването на гранично
разпределение получаваме Pn  e p', а преминаването в
граница на уравненията (16.6) води до e p'= e p'P.
Така се получава, че граничното разпределение p е ляв
(нетривиален) собствен вектор на P. Това означава, че ако в
даден момент веригата има такова разпределение, то ще се
запази неизменно и за в бъдеще.
e p', а преминаването в
граница на уравненията (16.6) води до e p'= e p'P.
Така се получава, че граничното разпределение p е ляв
(нетривиален) собствен вектор на P. Това означава, че ако в
даден момент веригата има такова разпределение, то ще се
запази неизменно и за в бъдеще.

16.3 Класификация на състоянията
Ще започнем тази тема с два тривиални примера.
Пример 16.1 Да разгледаме
следните матрици на преходни вероятности:
| P1= |
ж
и |
|
|
|
ц
ш |
, P2= |
ж
з
з
и |
|
|
|
ц
ч
ч
ш |
.
|
При матрицата P1 системата остава завинаги в състоянието 2,
когато го достигне. Такова състояние се нарича поглъщащо.
Понякога
цял клас състояния може да бъде поглъщащ -- веднъж достигнат
вече
не може да бъде напуснат. Поглъщащото състояние (или клас) може да се
достига в случаен момент на времето -- за тази конкретна верига
разпределението му е геометрично.
Състоянието 1 в този пример пък е такова, че веднъж напуснато
то не може да бъде достигнато никога. Състояние (или клас
състояния) с това свойство наричаме невъзвратни.
При матрицата P2 периодично се сменят три състояния в реда:
| 1,2,3,1,2,3,.. или |
| 2,3,1,2,3,1,.. или |
| 3,1,2,3,1,2,.. |
и всъщност цялата вероятностна мярка е съсредоточена
върху три траектории, започващи от различни начални състояния в
зависимост от вектора на началните вероятности p0. Бъдещото
поведение на такава верига става напълно предсказуемо --- то
детерминирано се определя от нейното настояще. Състояние от този
тип се нарича периодично. Естествено е, че състоянията, през
които преминава траекторията при своето периодично движение,
образуват периодичен клас състояния. Такъв клас е винаги
поглъщащ, но може, разбира се, да бъде достигнат в случаен момент
на времето. Състояние, което не принадлежи на никой периодичен
клас се нарича апериодично.
Изобщо казано състоянията на веригата могат да бъдат частично
наредени: казваме че състоянието i 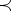 j, ако pi,jn > 0
за някое n. Ясно е, че еквивалентните състояния в тази наредба
образуват клас. Когато от класа не може да се излезе, класът е
максимален в указаната частична наредба. Една верига може да
има няколко такива класа.
Такъв клас ще наричаме ергодичен, а състоянията в него
ергодични.
j, ако pi,jn > 0
за някое n. Ясно е, че еквивалентните състояния в тази наредба
образуват клас. Когато от класа не може да се излезе, класът е
максимален в указаната частична наредба. Една верига може да
има няколко такива класа.
Такъв клас ще наричаме ергодичен, а състоянията в него
ергодични.
Класификацията на състояния представлява особен интерес в теорията
на Марковските вериги поради следните теореми:
Теорема 16.4
Възвратната апериодична Марковска верига е ергодична.
Всъщност не е трудно да се съобрази, че теоремата на Марков следва
от тази теорема --- периодичността и невъзвратността винаги са
свързани с наличието на нулеви вероятности. Така неговата матрица
с положителни елементи е матрица на ергодична верига.
Теорема 16.5
Граничното разпределение на ергодична Марковска верига е
единствено и не зависи от началното състояние.
16.4 Примери и задачи
Пример 16.2
''Канал с шум'' или Марковска верига с две
симетрични състояния.
Системата сменя състоянието си с вероятност p < 1/2
или остава в същото състояние с вероятност q=1-p. Тогава преходната матрица
P е симетрична. Нейната n-та степен Pn е също симетрична и
двете съответно имат вида:
Уравненията на Марков в този случай се записват просто:
|
1-pn |
= |
(1-p)(1-pn-1)+p pn-1 |
(16.7) |
|
pn |
= |
p(1-pn-1)+(1-p) pn-1. |
|
Чрез изваждане на второто уравнение от първото получаваме:
1-2pn = (1-2p) (1- 2pn-1)
1-2pn = (1-2p)n
Следователно получаваме, че pn  1/2. Така в този частен случай
граничното разпределение е равномерното.
1/2. Така в този частен случай
граничното разпределение е равномерното.

Пример 16.3
Неергодична верига.
Да разгледаме веригата със симетрична преходна матрица:
Да означим с p вектора от начални вероятности. Покажете, че
граничното разпределение (зависещо от началното) е
p1, (p2+p3)/2, (p2+p3)/2.
Д.Въндев -Теория на вероятностите - January 9, 2002



 Ґ pi,jn =pj независимо от индекса i.
Ґ pi,jn =pj независимо от индекса i.




 Ґ pi,jn =pj независимо от индекса i.
Ґ pi,jn =pj независимо от индекса i.

 e p', а преминаването в
граница на уравненията (16.6) води до e p'= e p'P.
Така се получава, че граничното разпределение p е ляв
(нетривиален) собствен вектор на P. Това означава, че ако в
даден момент веригата има такова разпределение, то ще се
запази неизменно и за в бъдеще.
e p', а преминаването в
граница на уравненията (16.6) води до e p'= e p'P.
Така се получава, че граничното разпределение p е ляв
(нетривиален) собствен вектор на P. Това означава, че ако в
даден момент веригата има такова разпределение, то ще се
запази неизменно и за в бъдеще.

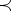 j, ако pi,jn > 0
за някое n. Ясно е, че еквивалентните състояния в тази наредба
образуват клас. Когато от класа не може да се излезе, класът е
максимален в указаната частична наредба. Една верига може да
има няколко такива класа.
Такъв клас ще наричаме ергодичен, а състоянията в него
ергодични.
j, ако pi,jn > 0
за някое n. Ясно е, че еквивалентните състояния в тази наредба
образуват клас. Когато от класа не може да се излезе, класът е
максимален в указаната частична наредба. Една верига може да
има няколко такива класа.
Такъв клас ще наричаме ергодичен, а състоянията в него
ергодични. 1/2. Така в този частен случай
граничното разпределение е равномерното.
1/2. Така в този частен случай
граничното разпределение е равномерното.



