The Normal Distribution
The Normal Distribution |
|
|
Simulation of the normal experiment
The normal distribution holds an honored role in probability and statistics, mostly because of the central limit theorem, one of the cornerstone results. In addition, as we will see, the normal distribution has many nice mathematical properties.
A random variable X is said to have the normal distribution with parameters
if it has the probability density function f given by
The special case
corresponds to the standard normal distribution. This particular distribution is so important that it has its own notation. The density is denoted
and the distribution function is denoted
The standard normal distribution function cannot be expressed in terms of elementary functions, and hence the values of this function have been approximated and are given in the table of the standard normal distribution.
1. Show that standard normal density
really is a probability density function by showing that
Hint: Convert the following double integral into polar coordinates:
2. Show that the general normal
density function really is a probability density function. Use
Exercise 1 and the standardizing transformation
3. Use basic calculus techniques to
draw a careful sketch of the general normal density function. In
particular, show that
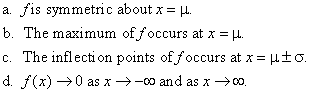
The applet for this page simulates a random variable with the normal distribution. The graph of the density function is shown in blue. The mean and standard deviation are recorded in the first table and shown graphically in terms of the horizontal blue bar, which is centered at the mean and extends one standard deviation on either side. You can vary the mean and standard deviation with a scroll bars. When you run the experiment, independent values of the normal distribution are generated and recorded in the second table. The empirical density function is graphed in red and the sample mean and variance recorded in the first table and shown graphically in terms of the horizontal red bar.
4. Start the applet and vary
the mean and standard deviation. Note the shape and location of
the normal density function and the location and size of the
mean-standard deviation bar.
5. Run the simulation with an update frequency
of 100 for several different degrees of freedom. Note the
apparent convergence of the empirical density and statistics to
the corresponding distribution density and parameters.
The important properties of the normal distribution are most easily obtained using the moment generating function.
6. If X has the general normal
density function, show that the moment
generating function of X is given by
As the notation suggests, the parameters are the mean and standard deviation, respectively.
7. Suppose that X has the
normal distribution with parameters
Show that
8. Suppose that X is normally
distributed. If a and b are constants and a
is nonzero, show that aX + b is normally distributed.
An important consequence of Exercise 6 is the following result:
9. Show that if X has the
normal distribution with
then
has the standard normal distribution.
10. Conversely, show that if Z has
the standard normal distribution, then
has the normal distribution with
Exercise 10 is very important because it means that any event that can be expressed in terms of X can also be expressed in terms of Z. Hence, the probability of such an event can be approximated using the table of the standard normal distribution.
11. Show that if X and Y
are independent, normally
distributed random variables, then X + Y is normally
distributed.
Special Distributions |
  |
