Random Variables |
Simulation of the dice experiment
Simulation of Buffon's coin experiment
Suppose that we have a random experiment with sample space S. A random variable X is a real-valued function defined on the sample space S of the experiment. More generally, a k-dimensional random vector X is a function from the sample space S into a subset T of Rk. Equivalently, X is a sequence of k random variables:
X = (X1, X2, ..., Xk)
Intuitively, you should think of a random variable as a measurement of interest in the context of the random experiment. Similarly, a random vector is a sequence of measurements. A random vector X is random in the sense that its value depends on the outcome of the experiment, which cannot be predicted with certainty before the experiment is run. Each time the experiment is run, an outcome s in S of the experiment occurs, and a given random vector X takes on the value X(s). In general, as you will see, the notation of probability suppresses references to the sample space.
![]() 1. Recall that the dice
experiment consists of rolling a pair of (distinct) fair
dice and recording the number spots showing on each die. Express
each of the following random variables as a function defined on
the sample space:
1. Recall that the dice
experiment consists of rolling a pair of (distinct) fair
dice and recording the number spots showing on each die. Express
each of the following random variables as a function defined on
the sample space:
![]() 2. Run the simulation of the
dice experiment 100 times. For each run, compute the value of
each of the random variables in Exercise 1.
2. Run the simulation of the
dice experiment 100 times. For each run, compute the value of
each of the random variables in Exercise 1.
![]() 3. Recall that Buffon's coin
experiment consists of tossing a coin with radius r
< 1 randomly on a floor covered with square tiles of side
length 1. The coordinates of the center of the coin are recorded
relative to axes through the center of the square, parallel to
the sides. Express each of the following random variables as a
function defined on the sample space:
3. Recall that Buffon's coin
experiment consists of tossing a coin with radius r
< 1 randomly on a floor covered with square tiles of side
length 1. The coordinates of the center of the coin are recorded
relative to axes through the center of the square, parallel to
the sides. Express each of the following random variables as a
function defined on the sample space:
![]() 4. Run the simulation of the
Buffon's coin experiment 100 times with r = 0.2. For
each run, compute the value of each of the random variables in
Exercise 3.
4. Run the simulation of the
Buffon's coin experiment 100 times with r = 0.2. For
each run, compute the value of each of the random variables in
Exercise 3.
Suppose that X is a random vector for an experiment with sample space S, and that X takes values in a subset T of Rk. Any statement about the random vector is an event. More precisely, the events that can be defined in terms of X have the form
![]() 5. In the dice experiment,
consider the variables defined in Exercise 1. Express each of the
following events in the form {X in B}
for a suitably chosen random vector X and subset
B. Then express each event explicitly as a subset of the
sample space.
5. In the dice experiment,
consider the variables defined in Exercise 1. Express each of the
following events in the form {X in B}
for a suitably chosen random vector X and subset
B. Then express each event explicitly as a subset of the
sample space.
![]() 6. In Buffon's coin experiment,
consider the random variables defined in Exercise 3. Express each
of the following events in the form {X in B}
for a suitably chosen random vector X and subset
B. Then express each event explicitly as a subset of the
sample space.
6. In Buffon's coin experiment,
consider the random variables defined in Exercise 3. Express each
of the following events in the form {X in B}
for a suitably chosen random vector X and subset
B. Then express each event explicitly as a subset of the
sample space.
In the following exercises, X is a random vector for an experiment with sample space S, and X takes values in a subset T of Rk. Suppose that B and C are subsets of T and Bi is a collection of subsets of T indexed by a countable set I.
![]() 7. Show that
7. Show that
![]() 8. Show that
8. Show that
![]() 9. Show that
9. Show that
![]() 10. Show that
10. Show that
![]() 11. Show that if B and C
are disjoint, then so are
11. Show that if B and C
are disjoint, then so are
By Exercises 7-11, the mapping
from subsets of T to subsets of S preserves all of the set operations.
Suppose again that X is a random vector for the experiment with sample space S and that X takes values in subset T of Rk.
![]() 12. Use the results of Exercises
7-11 to show that the mapping
12. Use the results of Exercises
7-11 to show that the mapping
on subsets of T defines a probability measure on T. This is called the probability distribution of X.
Thus, note that any random vector X for an experiment reproduces the basic structure of the probability space:
![]() 13. In the dice experiment,
consider the variables defined in Exercise 1. Find the
probability of each of the following events (see also Exercise
5):
13. In the dice experiment,
consider the variables defined in Exercise 1. Find the
probability of each of the following events (see also Exercise
5):
![]() 14. Run the dice experiment 100 times. Compute
the relative frequency of each of the events in Exercise 13.
14. Run the dice experiment 100 times. Compute
the relative frequency of each of the events in Exercise 13.
![]() 15. In Buffon's coin experiment,
consider the variables defined in Exercise 3. Find the
probability of each of the following events (see also Exercise
5):
15. In Buffon's coin experiment,
consider the variables defined in Exercise 3. Find the
probability of each of the following events (see also Exercise
5):
![]() 16. Run Buffon's coin experiment 100 times.
Compute the relative frequency of each of the events in Exercise
15.
16. Run Buffon's coin experiment 100 times.
Compute the relative frequency of each of the events in Exercise
15.
For any event A, there is a simple random variable called the indicator variable of A, whose value tells us whether or not A has occurred:
1A(s) = 1 for s in A; 1A(s) = 0 for s in Ac.
or more simply, in the language of the experiment,
1A = 1 if A occurs; 1A = 0 if A does not occur
![]() 17. Conversely, show that any
random variable I that just takes the values 0 and 1 is
the indicator variable of the event
17. Conversely, show that any
random variable I that just takes the values 0 and 1 is
the indicator variable of the event
![]() 18. In the dice experiment, let
A denote the event that the sum of the scores is 7. Run
the simulation 100 times, and for each run, compute the value of 1A.
18. In the dice experiment, let
A denote the event that the sum of the scores is 7. Run
the simulation 100 times, and for each run, compute the value of 1A.
![]() 19. In Buffon's coin
experiment, let A denote the event that the coin does
not touch the sides of the square. Run the simulation 100 times
with r = 0.2 and for each run, compute the value of 1A.
19. In Buffon's coin
experiment, let A denote the event that the coin does
not touch the sides of the square. Run the simulation 100 times
with r = 0.2 and for each run, compute the value of 1A.
![]() 20. Let A and B be
events in a random experiment. Show that
20. Let A and B be
events in a random experiment. Show that
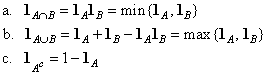
![]() 21. Suppose that we have a
collection of events Ai for an
experiment, indexed by a countable set I. Show that
21. Suppose that we have a
collection of events Ai for an
experiment, indexed by a countable set I. Show that
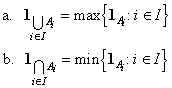
Recall that the outcome of a random experiment is usually a sequence of a fixed number n of real measurements, so that the sample space S is a subset of Rn. Thus, the outcome of the experiment itself can be thought of as a random vector. Let X denote the identity function on S:
X(s) = s for s in S
Then X is a random vector and the components of X are random variables that give the individual measurements. That is,
X = (X1, X2, ..., Xn) where Xi(s) = si for s in S.
The events that can be defined in terms of X are simply the events of the experiment; that is
If Y is another random vector for the experiment, taking values in a subset T of Rk, then Y is a function of X. That is, there is a function g from S into T such that
Y = g(X) so that Y(s) = g(X(s)) for s in S
We could refer to X as the basic outcome variable and Y as a derived variable.
![]() 22.In the dice experiment,
consider the random variables defined in Exercise 1. By
definition, the basic outcome vector is the vector of dice scores
(X, Y). Express each of the following as a
function of (X, Y).
22.In the dice experiment,
consider the random variables defined in Exercise 1. By
definition, the basic outcome vector is the vector of dice scores
(X, Y). Express each of the following as a
function of (X, Y).
![]() 23.In Buffon's coin experiment,
consider the random variables defined in Exercise 3. By
definition, the basic outcome vector is the position of the coin
center (X, Y). Express each of the following as
a function of (X, Y).
23.In Buffon's coin experiment,
consider the random variables defined in Exercise 3. By
definition, the basic outcome vector is the position of the coin
center (X, Y). Express each of the following as
a function of (X, Y).
In many problems of elementary probability theory, the basic object of interest is a random vector X taking values in a subset T or Rk for some k. Whether X is the basic outcome vector or a derived vector is often irrelevant.
Probability Spaces |