Probability Measure

Simulation of the dice experiment

Simulation of Buffon's coin experiment

Suppose that we have a random experiment with sample space S. The probability of an event is a measure of how likely the event is to occur when the experiment if run.

Axioms

Mathematically, a probability measure P is a real-valued function defined on the collection of events of a random experiment that satisfies the following axioms:

1. P(A) is nonnegative for any event A.
2. P(S) = 1
3. If A_i for i in I is a countable collection of pairwise disjoint events, then

Axiom 3 is known as countable additivity.

Finite measures

Axioms 1 and 2 are really just a matter of convention; we choose to measure the probability of an event with a number between 0 and 1 (as opposed, say, to a number between 0 and 100). Axiom 3 however, is fundamental and inescapable. It is required for probability for precisely the same reason that it is required for other measures of the "size" of a set:

• Counting measure # defined on the subsets of a finite set S.
• Length measure defined on the subsets of a bounded interval S in R.
• Area measure defined on the subsets of a set S of R² with finite area.
• Volume measure defined on the subsets of a set S of R³ with finite volume.

Each of these measures is a finite measure, that is, a real-valued function m defined on the subsets of S that satisfies axioms 1 and 3, but not necessarily axiom 2; m(S) is only required to be finite.

1. Show that if m is a finite measure then the function P defined by

P(A) = m(A) / m(S)

is a probability measure.

Law of large numbers

Intuitively, the probability of an event is supposed to measure the long-term relative frequency of the event. Specifically, suppose that A is an event in an experiment that is run repeatedly. Let

N_n(A) denote the number of times A occurred in the first n runs

so that

N_n(A) / n is the relative frequency of A in the first n runs

If we have modeled the experiment correctly, then in some sense we expect that the relative frequency of A should converge to the probability of A as n increases. The precise statement of this is the law of large numbers, one of the fundamental theorems in probability.

Examples

Suppose that the dice in the dice experiment are fair. We have no reason to prefer one outcome over another, so the probability of an event should be proportional to the number of elements in the event. Thus, a good choice for the probability measure might be

P(A) = #(A) / #(S) for any subset A of S

By Exercise 1, this really is a probability distribution. In the remainder of the chapter, we will assume that this distribution is correct.

2. In the dice experiment, let A denote the event that the first die score is less than 4 and B the event that the sum of the dice scores is 7. Find the probability of the following events

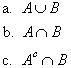
3. Run the simulation of the dice experiment 100 times. Compute the relative frequency of each event in Exercise 2.

In Buffon's coin experiment, if the coin is tossed "randomly" on the floor, then we have no reason to prefer one part of the square over another. Thus, the probability of an event should be proportional to the area of the event, so a good choice for the probability measure might be

P(A) = area(A) / area(S) for any subset A of S

By Exercise 1, this really is a probability distribution. In the remainder of the chapter, we will assume that this distribution is correct.

4. In Buffon's coin experiment, let A denote the event that the coin does not touch the sides of the square. Find the probability of the following events:

1. A^c
2. A

5. Run the simulation of Buffon's coin experiment 100 times. Compute the relative frequency of each event in Exercise 4.

Basic rules of probability

Suppose that we have a random experiment with sample space S and probability measure P. Use the axioms of probability to verify the following basic properties:

6. Show that P(A^c) = 1 - P(A)

7. Show that P(Ø) = 0.

8. Show that

9. Show that if A is a subset of B then

10. Show that if A is a subset of B then

11. Show that

12. Show that

Exercises 6 and 7 can be generalized to a union of n events

A_i, where i is in I = {1, 2, ..., n}

This very important result is known as the inclusion-exclusion rule:

13. Show that

The next two results are known as the continuity theorems.

14. Consider an increasing sequence of events:

Show that

15. Consider a decreasing sequence of events:

Show that

If you go back and look at your proofs in Exercise 6-15, you will see that they hold for any finite measure, not just probability. Only the complement rule 6 changes; it becomes

m(A^c) = m(S) - m(A)

In particular, the inclusion-exclusion rule is as important in combinatorics (the study of counting measure) as it is in probability.

More Exercises

16. Suppose that A and B are events in an experiment with

Express each of the following events in the language of the experiment and find its probability:

17. Suppose that A, B, and C are events in an experiment with

Express each of the following events in set notation and find its probability:

1. At least one of the three events occurs.
2. None of the three events occurs.
3. Exactly one of the three events occurs.
4. Exactly two of the three events occur.

Probability Spaces