Sample Spaces and Events

Simulation of the dice experiment

Simulation of Buffon's coin experiment

Set theory is the foundation of probability, as it is for almost every branch of mathematics. In probability, set theory is used to provide a language for modeling and describing random experiments.

Sets and subsets

First, a set is simply a collection of objects; the objects are referred to as elements of the set. The statement that s is an element of set S is written

If A and B are sets then by definition, A is a subset of B if every element of A is also an element of B:

By definition, a set is completely determined be its elements. Thus sets A and B are equal if they have the same elements:

In most applications of set theory, all sets under discussion are subsets of a certain universal set. By contrast, the empty set, denoted Ø, is the set with no elements.

1. Use the formal definition of implication to show that the empty set is a subset of any set A.

Sample Space and Events

For a random experiment, the set S of all possible outcomes of the experiment is called the sample space of the experiment. Thus, the sample space plays the role of the universal set when modeling the experiment.

Subsets of the sample space of an experiment are referred to as events. Thus, an event is a set of possible outcomes of the experiment. Each time the experiment is run, a given event A either occurs, if the outcome of the experiment is an element of A, or does not occur, if the outcome of the experiment is not an element of A. Intuitively, you should think of an event as a meaningful statement about the experiment.

Note that the sample space S itself is an event; by definition it always occurs. More generally, if A and B are events in the experiment and A is a subset of B, then the occurrence of A implies the occurrence of B. As an event in a random experiment, the empty set never occurs.

Product sets

Usually, the outcome of a random experiment consists of one or more real measurements, and thus, the sample space consists of all possible measurement sequences. Thus, we need good notation for constructing sets of sequences. The Cartesian product of sets S₁, S₂, ..., S_n, denoted

S₁ × S₂ × ··· × S_n

is the set of all (ordered) sequences (s₁, s₂ , ..., s_n) where s_i is an element of S_i for each i. By definition, two ordered sequences are the same if and only if their corresponding coordinates agree:

(s₁, s₂ , ..., s_n) = (t₁, t₂ , ..., t_n) if and only if s_i = t_i for i = 1, 2, ..., n.

If all the sets in the product are the same, then we denote the product by

Sⁿ = S × S × ··· × S (n factors)

In particular, R will denote the set of real numbers so that Rⁿ is n-dimensional Euclidean space. Thus, in most cases, the sample space of a random experiment, and hence the events of the experiment, are subsets of Rⁿ for some n.

2. Recall that the dice experiment consists of rolling a pair of (distinct) dice and recording the number spots showing on each die.

1. Define the sample space S mathematically.
2. Let A denote the event that the first die score is less than 4. Express A mathematically.
3. Let B denote the event that the sum of the dice scores is 7. Express B mathematically.

3. Run the simulation of the dice experiment 100 times. Count the number of times each of the events in Exercise 2 occurred.

4. Recall that Buffon's coin experiment consists of tossing a coin with radius r < 1 on a floor covered with square tiles of side length 1. The coordinates of the center of the coin are recorded relative to axes through the center of the square, parallel to the sides.

1. Define the sample space S mathematically.
2. Let A denote the event that the coin does not touch the sides of the square. Describe A mathematically.

5. Run the simulation of the Buffon's coin experiment 100 times. Count the number of times the event A in Exercise 4 occurred.

6. Suppose that we have n experiments E₁, E₂, ..., E_n with sample spaces S₁, S₂, ..., S_n, respectively. Give the sample space of the compound experiment that consists performing the n experiments in sequence.

7. Suppose that we have a basic experiment with sample space S. Give the sample space of the compound experiment that consists of n replications of the basic experiment.

Set operations

We are now ready to review the basic operations of set theory. For a random experiment, these operations can be used to construct new events from given events. For the following definitions, suppose that A and B are subsets of the universal set, which we will denote by S.

Union

The union of A and B is the set obtained by combining the elements of A and B.

If A and B are events in an experiment with sample space S, then the union of A and B is the event that occurs if and only if A occurs or B occurs.

Intersection

The intersection of A and B is the set of elements common to both A and B:

If A and B are events in an experiment with sample space S, then the intersection of A and B is the event that occurs if and only if A occurs and B occurs.

If the intersection of sets A and B is empty, then A and B are said to be disjoint:

If A and B are disjoint events in an experiment, then they are mutually exclusive; they cannot both occur on the same run of the experiment.

Complement

The complement of A is the set of elements that are not in A and is denoted A^c.

If A is an event in an experiment with sample space S, then the complement of A is the event that occurs if and only if A does not occur.

8. In the dice experiment, consider the events A and B of Exercise 2. List the outcomes in the following events.

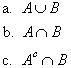
9. Run the simulation of the dice experiment 100 times. Count the number of times each of the events in Exercise 8 occurred.

10. In Buffon's coin experiment, consider the event A of Exercise 4. Describe mathematically the event A^c.

11. Run the simulation of Buffon's coin experiment 100 times. Count the number of times A^c occurred.

Basic rules

In the following problems, A, B, and C are subsets of a universal set S.

12. Show that

13. Prove the commutative laws:

14. Prove the associative laws:

15. Prove the distributive laws:

16. Prove DeMorgan’s laws:

General constructions

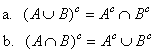
A set is said to countable if it can be put into one-to-one correspondence with a subset of the integers. Thus, a countable set is either finite or an infinite sequence. By contrast, the set of real numbers is not countable. As we will see, countable sets play a special role in probability, because we often need to construct a new event from a countable collection of given events.

The operations of union and intersection can easily be extended to a finite or even an infinite collection of sets. Thus, suppose that we have a collection of subsets A_i of a universal set S, indexed by i in a countable set I:

Union

The union of the collection is the set obtained by combining the elements of the given sets:

If the given sets are events in an experiment with sample space S, then the union is the event that occurs if and only if at least one event in the collection occurs.

Intersection

The intersection of the collection is the set of elements common to all sets in the collection:

If the sets in the collection are events in an experiment with sample space S, then the intersection is the event that occurs if and only if every event in the collection occurs.

The collection of sets is pairwise disjoint if the intersection of any two sets in the collection is empty:

If the sets are events in a random experiment, this means that they are mutually exclusive; at most one of the events could occur on a given run of the experiment.

In the following problems, I is a countable index set, and sets A and B_i for i in I are subsets of a universal set S.

Basic Rules

17. Prove the general distributive laws:

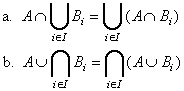
18. Prove the general De Morgan’s laws:

Measurable Sets

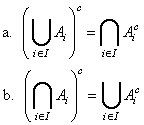
The sets in this text are assumed to be subsets of Rⁿ for some n. We will also assume that the sets are measurable. This means that each set is either a product set of the form

A₁ × A₂ × ··· × A_n where A_i is an interval of R for each i

or a set that can be constructed from product sets with a countable number of set operations. This assumption rules out certain weird sets that would otherwise complicate the theory.

Probability Spaces