Conditional Probability

Simulation of the dice experiment

Simulation of Buffon's coin experiment

Definition

Suppose that we know that an event B in a random experiment has occurred. In general, this information should clearly alter probabilities that we assign to other events. In particular, if A is another event then A occurs if and only if A and B occur. Thus, the probability of A, given that we know B has occurred, should be proportional to

However, conditional probability, given that B has occurred, should still be a probability measure, that is, it must satisfy the axioms of probability. This forces the proportionality constant to be 1/P(B). Thus, we are led inexorably to the following definition:

Let A and B be events in a random experiment with P(B) > 0. The conditional probability of A given B is defined to be

This argument was based on the axiomatic definition of probability. Let’s explore the idea of conditional probability from the less formal and more intuitive notion of relative frequency. Thus, suppose that we replicate the experiment repeatedly. For an arbitrary event C, let

N_n(C)

denote the number of times C occurs in the first n runs.

If N_n(B) is large, the conditional probability that A has occurred given that B has occurred should be close to the conditional relative frequency of A given B, namely the relative frequency of A for the runs on which B occurred:

But by another application of the relative frequency idea,

so again we are led to the same definition.

1. Suppose that A and B are events in an experiment with

Find each of the following:

1. P(A | B)
2. P(B | A)
3. P(A^c | B)
4. P(B^c | A)
5. P(A^c | B^c)

2. Recall that the dice experiment consists of rolling a pair of (distinct) fair dice and recording (X, Y) where X is the score on die 1 and Y is the score on die 2. Let Z = X + Y denote the sum of the scores. Find each of the following:

1. P(X = 3 | Z = 6)
2. P(X = 3 | Z = 7)
3. P(X < 3 | Z > 7)

3. Run the simulation of the dice experiment 500 times. Compute the conditional relative frequencies corresponding to the conditional probabilities in Exercise 2.

4. Recall that Buffon's coin experiment consists of tossing a coin with radius r < 1 randomly on a floor covered with square tiles of side length 1. The coordinates (X, Y) of the center of the coin are recorded relative to axes through the center of the square, parallel to the sides. Find

P(Y > 0 | X < Y)

5. Run the simulation of the Buffon's coin experiment 500 times. Compute the conditional relative frequencies corresponding to the conditional probability in Exercise 4.

Properties

6. Show that as a function of A, for fixed B, P(A | B) is a probability measure.

Exercise 6 is the most important property of conditional probability and it means that any result that holds for probability measures in general holds for conditional probability, as long as the conditioning event remains fixed.

7. Suppose that A and B are events in a random experiment and that B has positive probability. Prove each of the following mathematically and interpret each in the language of the experiment:

1. If B is a subset of A then P(A | B) = 1.
2. If A is a subset of B then P(A | B) = P(A) / P(B).
3. If A and B are disjoint then P(A | B) = 0.

8. Suppose that A and B are events in a random experiment, each having positive probability. Show that

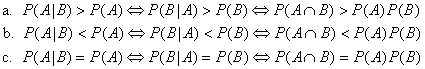
In case a, A and B are said to be positively correlated. Intuitively, the occurrence of either event means that the other event is more likely. In case b, A and B are said to be negatively correlated. Intuitively, the occurrence of either event means that the other event is less likely. In case c, A and B are said to be independent. Intuitively, the occurrence of either event does not change the probability of the other event.

9. Refer to Exercise 2 on the dice experiment. Determine whether each of the following pairs of events are positively correlated, negatively correlated, or independent. Think about the results

1. {X = 3}, {Z = 6}
2. {X = 3}, {Z = 7}
3. {X < 3}, {Z > 7}

Sometimes conditional probabilities are known and can be used to find the probabilities of other events.

10. Prove the multiplication rule of probability.

(Assume that the conditioning events have positive probability.)

Compare the multiplication rule of probability with the multiplication rule of combinatorics.

11. An urn contains 25 balls, 15 are red and 10 are green. Five balls are chosen at random, without replacement. Find the probability that the first, third, and fifth balls are red and the second and fourth are green.

Conditional Distributions

Suppose that X is a random vector for an experiment with sample space S and probability measure P, and that X takes values in subset T of R^k. Recall that the probability distribution of X is the mapping

on subsets B of T. Analogously, if A is an event (a subset of S) with positive probability, the conditional distribution of X given A is the mapping that

on subsets B of T.

12. In the dice experiment, find the conditional distribution of (X, Y) given that X + Y = 7.

13. In Buffon's coin experiment, find the conditional distribution of (X, Y) given that the coin does not touch the sides of the square.

Probability Spaces