Distribution Functions

Definition

Let X be a random variable. The (cumulative) distribution function of X is the function F given by

This function is important because it makes sense for any type of real-valued variable--discrete, continuous, or even mixed, and because as we will see, it completely determines the distribution of X. We will abbreviate some limits of F as follows:

Basic Properties

The properties in the following exercises completely characterize distribution functions. The continuity theorems will be helpful in the proofs.

1. Show that F is increasing:

if x y then F(x) F(y)

2. Show that F is continuous from the right:

F(x⁺) = F(x) for each x in R.

3. Show that F has limits from the left:

F(x^-) = P(X < x) for each x in R.

4. Show that

5. Show that

The following exercise shows how the distribution function can be used to compute the probability that X is in an interval. Using this result and the rules of probability we can, in principal, find the probability that X is in an arbitrary set that can be constructed from a countable number of intervals. Thus, the distribution function determines the distribution of X.

6. Suppose that a and b are in R with a < b. Show that

1. P(X = a) = F(a) - F(a^-)
2. P(a < X b) = F(b) - F(a)
3. P(a < X < b) = F(b^-) - F(a)
4. P(a X b) = F(b) - F(a^-)
5. P(a X < b) = F(b^-) - F(a^-)

Relation to Density Functions

In the case that X is discrete, there is a simple relationship between the distribution function and the density function.

3. Suppose that X is discrete with density function f and distribution function F. Show that for x in R,

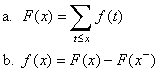
Thus, F is a step function with jumps at the values of X that have positive probability; the size of the jump at x is the density function at x.

There is an analogous result when X is continuous.

4. Suppose that X is continuous with density function f and distribution function F. Show that

Quantiles

A value of x such that

F(x^-) = P(X < x) 1 / 2 and F(x) = P(X x) 1 / 2

is called a median of the distribution. When there is only one median, it is sometimes used as a measure of the center of the distribution. More generally, suppose that p is in (0, 1). A value of x such that

F(x^-) = P(X < x) p and F(x) = P(X x) 1 - p

is called a quantile of order p for the distribution. Thus, the median is the quantile of order 0.5

5. Suppose that X is continuous and takes values in an interval I and that F is strictly increasing on I. Show that for each p in (0, 1), X has a unique quantile of order p.

6. Suppose that X has the power distribution with parameter a > 1, which has probability density function

f(x) = (a - 1)x^-a for x > 1

Find the distribution function of X and find the median, the quantile of order 0.25 and the quantile of order 0.75.

Right Tail Functions

A function that clearly gives the same information as the distribution function is the right-tail probability function:

G(x) = 1 - F(x) = P(X > x) for x in R

Sometimes this function is more natural, particularly in the reliability setting in which X represents the lifetime of a device.

Functions of a Random Variable

Distribution functions are useful for finding the probability density function of a continuous random variable Y that is a function of another random variable X. The general technique is to find the distribution function of Y, using the basic rules of probability, and then differentiate to get the density function.

7. Suppose that X is uniformly distributed on the interval (–2, 2). Find the density function of

Y = X²

When the function of random variable X is one-to-one, there is a simple formula that gives the density of Y in terms of the function and the density of X. This is known as the change of variables formula.

8. Suppose that X is continuous random variable taking values in an interval S of R and that X has probability density function f. Suppose that Y = r(X) where r is a strictly monotone (increasing or decreasing) function from S onto an interval T. Finally, assume that the inverse function

x = r^-1(y)

has a nonzero derivative on T. Show that the density g of Y is given by

The two-dimensional version of the change of variables formula is derived in the Bivariate Distributions discussion.

9. Suppose that X is uniformly distributed on the interval (2, 4). Find the density function of

Y = X²

10. Suppose that X has the density function

f(x) = x² / 3 for –1 < x < 2

Find the density function of Y = X^1/3.

11. Suppose that X has the power distribution with parameter a > 1, which has density function

f(x) = (a - 1)x^-a for x > 1

Find the density function of Y = 1 / X.

12. Suppose that X₁, X₂, ..., X_n are independent random variables and that X_i has distribution function F_i for each i. Let Y = min{X₁, X₂, ..., X_n} and let G denote the distribution function of Y.

1. Show that for any t,

1 - G(t) = [1 - F₁(t)][1 - F₂(t)]···[1 - F_n(t)]

2. In particular, suppose that the X_i are identically distributed with common distribution function F. Show that

G(t) = 1 - [1 - F(t)]ⁿ

3. Suppose that the X_i are continuous random variables with common density f. Show that the density function g of Y is given by

g(t) = n[1 - F(t)]^n-1f(t)

13. Suppose that X₁, X₂, ..., X_n are independent random variables and that X_i has distribution function F_i for each i. Let Z = max{X₁, X₂, ..., X_n} and let H denote the distribution function of Z.

1. Show that for any t,

H(t) = F₁(t) F₂(t) ··· F_n(t)

2. In particular, suppose that the X_i are identically distributed with common distribution function F. Show that

H(t) = [F(t)]ⁿ

3. Suppose that the X_i are continuous random variables with common density f. Show that the density function h of Z is given by

h(t) = n[F(t)]^n-1f(t)

Distributions