Лекция 10
Полиномна регресия

Това е една много популярна форма на линейната регресия, при която за регресионен модел се използуват полиноми. При нея се прибягва, когато нямаме априорни познания за аналитичната форма на модела. На долните картинки са показани типични данни от този случай.

polynoms.gif
Фигура 10.1: Криволинейни данни

В тази лекция си поставяме следните цели

Полиномният модел може да се запише във формата:

yi = a0+a1xi+a2xi2+...+anxin+ei.
(10.1)
Доказахме в предните лекции, че най - доброто решение за апроксимация на модела спрямо данните е методът на най - малките квадрати (МНК).

10.1  Населението на САЩ

Ще разгледаме един пример. Числата 75.995 91.972 105.711 123.203 131.669 150.697 179.323 203.212 226.505, са публикувани от Американския статистически институт и представляват населението (в милиони хора) на САЩ за периода от 1900 до 1980 г. Нека си поставим за задача да прогнозираме населението за две последователни десетилетия напред - 1990 и 2000. Като базисен ще разгледаме модела (10.1). Ясно е, че ще трябва да се ограничим с n Ј 8, тъй като разполагаме с 9 наблюдения и последния полином става интерполиращ.

За конкретния случай матрицата X изглежда така:

100000000
111111111
1248163264128256
139278124372921876561
141664256102440961638465536
152512562531251562578125390625
163621612967776466562799361679616
17493432401168071176498235435764801
1864512409632768262144209715216777216

Оценката (8.4) XўX [^(a)] = Xўy се получава като решение на системата уравнения:

е
 		yi
=
a0n+a1 е
 		xi+a2 е
 		xi2+,...,+an е
 		xin
е
 		xiyi
=
a0 е
 		xi+a1 е
 		xi2+a2 е
 		xi3+,..., +an е
 		xin+1
...
е
 		xin yi
=
a0 е
 		xin+a1 е
 		xin+1+a2 е
 		xin+2+,..., +an е
 		xin+n.
Приготвянето на такава матрица изисква пресмятането на твърде голям брой суми. Така изглежда XўX, даже ако забравим последните няколко колони, т.е. разглеждаме полином от по - ниска степен. Затова по - лесно е решението системата Xa = y, например, чрез използуването на (Singular Value Decomposition). Именно по този начин в демонстрационната програма census.m на системата MATLAB се решава този пример.

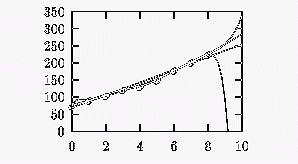
us.gif
Фигура 10.2: САЩ 1900 - 1980

На фигурата 10.2 са представени оригиналните данни, заедно с няколко регресионни полинома - от степени 1,2,6,8. Най-очевидно е несъответствието на прогнозираната стойност за полинома от 8 степен, който предсказва изчезване на цялото население на САЩ преди 2000 г. Пресмятанията са вършени с двойна точност така, че на резултатите от изчисленията може да се вярва. На долните таблици ще видим най - същественото от тези числени сметки. Главната цел, обаче е да въведем математическия апарат, който ще ни помогне да изберем ''оптималния'' от тези полиноми.

10.2  Ортогонални полиноми

Полиномите от произволна степен образуват линейно пространство. Нека разгледаме върху това пространство скаларно произведение зададено във формата:
(P,Q) = N
е
 i = 1 
 P(xi)Q(xi).
Тук с N голямо сме означили броя на данните.

Определение 1 Казваме, че два полинома са ортогонални (P^Q), ако (P,Q) = 0.

Теорема 1 Ще построим конструктивно редица от ортогонални полиноми: P0(x) = 1, P1(x) = x-[`(x)], а всички останали (при n < N) със следната рекурентна формула:

Pn(x) = (x-an) Pn-1(x) + bn Pn-2(x).
(10.2)

Доказателство: Да отбележим, че (P0,P1) = 0. Ще покажем първо, как може да се определят числата an,bn.

0 = (Pn,Pn-1) = (x Pn-1,Pn-1)-an(Pn-1,Pn-1)
0 = (Pn,Pn-2) = (x Pn-1,Pn-2)+bn(Pn-2,Pn-2)
Да отбележим, че от индукцията следва формулата:
(x Pn-1,Pn-2) = (Pn-1,x Pn-2) = (Pn-1,Pn-1).
От тук получаваме равенствата:
an =
n
е
 i = 1 
 xi Pn-12(xi)
n
е
 i = 1 
 Pn-12(xi)
(10.3)
bn = -
n
е
 i = 1 
 Pn-12(xi)
n
е
 i = 1 
 Pn-22(xi)
(10.4)
Сега ще покажем, че така получения полином е ортогонален и на всички полиноми с по - ниска степен (j < n-2):
(Pn,Pj) = (x Pn-1,Pj) = (Pn-1,xPj) = (Pn-1,Pj+1) = 0.
Q.E.D.

Така построената редица има смисъл, разбира се, докато степента на полинома е малка по сравнение с броя на данните N. Не е трудно да се провери, че Pj, j і N-1 има за корени числата xi.

Сега моделът (10.1) може да се препише във формата:

yi = b0P0+b1xi+b2P2(xi)+...+bnPn(xi)+ei.
(10.5)

Матрицата XўX за този модел е диагонална и съдържа числата dii = еPi-12(xi).

За нашия случай матрицата X изглежда така (това са стойностите на ортогоналните полиноми върху данните):

P0P1P2P3P4P5P6P7P8
1-49.3333-16.824.0000-26.666721.8182-11.74833.1329
1-32.33338.4-36.000073.3333-92.727370.4895-25.0629
1-2-2.666715.6-18.8571-26.6667120.0000-164.475587.7203
1-1-5.666710.815.4286-60.00005.4545164.4755-175.4406
10-6.6667-0.030.85710.0000-109.0909-0.0000219.3007
11-5.6667-10.815.428660.00005.4545-164.4755-175.4406
12-2.6667-15.6-18.857126.6667120.0000164.475587.7203
132.3333-8.4-36.0000-73.3333-92.7273-70.4895-25.0629
149.333316.824.000026.666721.818211.74833.1329

Коефициентите на ортогоналните полиноми са показани в следната таблица (редовете са степени на полинома (0 - 8 ), на диагонала е коефициентът пред максималната степен):

1.
-4. 1.
9.333 - 8. 1.
-16.8 36.2 -12. 1.
24.0 -124.57 79.5714 -16. 1.
-26.666372.88 -393.33 139.44 -20. 1.
21.818-1077.82 1664.91 -894.55 215.91-24.1.
-11.7483277.01 -6623.4684848.16 -1701.53309.077-28. 1.
3.132-10953.0826423.99-24217.8511220.28 -2889.6 419.067-32.1.

Коефициентите на разлагането на отклика bk по този нов базис са дадени в последната таблица.

10.3  Оптимална степен

Нека съгласно секция 9 се опитаме да оценим ''най - добрия'' регресионен полином. Ще построим редицата от подпространства Zi, i = 0,1,2,...,n. Подпространството Zi ще съответствува на полином от степен i и неговата размерност е i+1. Ясно е, че проверката на хипотезата H0:q О Zn-1 срещу сложната алтернатива H1:q О Zn\Zn-1 е еквивалентна на проверката an = 0 в модела (10.1) или на проверката bn = 0 в модела (10.5), когато, обаче този модел е верен. Това налага да търсим ''верната'' степен, започвайки отгоре - от максималната възможна степен. Това е n = N-2. За щастие изчислителните формули в модела (10.5) са изключително прости. За да ги изведем, нека въведем норма ||P||2 = (P,P) и означим с [(P)\tilde]k = Pk/||Pk||, k = 0,1,2,...,N-1 ортонормираните полиноми. Тогава N - мерното векторно пространство на наблюденията (y О RN) се представя в нова координатна система с вектори - стойностите на ортогоналните полиноми:
y = N-1
е
 k = 0 
 ~
b
 
k 
 ~
P
 
k 
 ,    ~
b
 
k 
 = (y, ~
P
 
k 
 )
||y||2 = N
е
 i = 1 
 yi2 = N-1
е
 k = 0 
 ~
b
 
 2
k 
 .
Последното равенство е всъщност равенството на Парсевал:
||y||2 = N
е
 i = 1 
 xi2,
където xi са координатите на вектора x в който и да е ортонормиран базис. При това връзката между коефициентите е тривиална:

~
b
 
k 
 = ||Pk|| ^
b
 
k 
 .

От тези равенства следват и търсените формули:

^
b
 
k 
 =
N
е
 i = 1 
 yi Pk(xi)
N
е
 i = 1 
 Pk2(xi)
 ,
(10.6)
s2( ^
b
 
k 
 ) =
^
s
 
 2
 
N
е
 i = 1 
 Pk2(xi)
 ,
(10.7)
^
s
 
 2
 
 = 1
N-n-1
 N-1
е
 k = n+1 
 ~
b
 
 2
k 
 = 1
N-n-1
 N-1
е
 k = n+1 
 ^
b
 
 2
k 
 N
е
 i = 1 
 Pk2(xi).
(10.8)
Тъй като частното:
fn =
~
b
 
 2
n 
1/(N-n-1) N-1
е
 k = n+1 
 ~
b
 
 2
k 
=
(N-n-1) ^
b
 
 2
n 
 N
е
 i = 1 
 Pn2(xi)
N-1
е
 k = n+1 
 ^
b
 
 2
k 
 N
е
 i = 1 
 Pk2(xi)
съгласно теорема 8.1 има F - разпределение с 1 и N-n-1 степени на свобода, правилото за проверка се свежда до намиране на минималното n, за което е изпълнено неравенството:

fn > Fкр.(1, N-n-1).

В долната таблица са изведени данните, необходими за намирането на ''оптималния'' полином за нашия пример. В последната колона за удобство са поставени критичните стойности за съответното F-разпределение. Вижда се, че максималната статистически значима степен е 2.

bk[(b)\tilde]k2F-valueDfF0.95
P0143.143184409.361.5251 85.32
P118.508 20552.7287.85281 7 5.59
P21.04582336.87 18.358 1 65.98
P3.10442615.546 0.81392 1 56.60
P4-.0769534.838 2.52819 1 47.70
P5-.0255513.575 0.97661 1 310.13
P6.00955 5.373 0.4797011 218.51
P7.01277 19.31 6.23907 1 1161.45
P8-.004953.095

От същата таблица се вижда също, че никаква статистическа проверка не е възможна за интерполационния полином от 8 степен. С указаните данни изобщо не е възможна проверка на адекватността на регресионния модел (с полином от 2-ра степен), така че използуването му за прогноза едва ли е оправдано.

Числата от последната колона са взети от таблица на квантилите на F-разпределение. Те се използуват за да се сравнят с тях стойностите на съответните статистики, дадени в колона 3. Когато става въпрос за програми, пресмятането на квантили е обикновено по - трудно от пресмятането на ф.р. Затова обикновено е автоматизирано пресмятането на вероятността: an = P (x < fn) , (x е сл.в. със съответното разпределение). Тя носи названието F - probability и така лесно можем да проверим за дадено ниво на доверие (например, a = 0.95) дали съответната хипотеза се отхвърля. Правилото за избор на оптимална степен съответно става: n = max{k: ak > a}.



Начало на лекцията | Съдържание | Индекс

File translated from TEX by TTH, version 2.10.
On 5 Apr 1999, 17:47.