Лекция 9
Проверки на хипотези в регресията

В тази лекция ще експлоатираме безпощадно теорема 8.2 и ще конструираме множество популярни хипотези в линейната регресия. В някои частни случаи конструираните доверителни области (поради естествените ''широки'' алтернативни хипотези) ще станат и доверителни интервали за неизвестните параметри.

9.1  Коефициент на детерминация

Коефициент на детерминация или проверка на наличието на линейна връзка между X и y.

Нека разгледаме сега регресионен модел със свободен член:

y = Xa + b ®
1
 
 + e,
(9.1)
където b е ''нов'' неизвестен параметър, а [1\vec] е n-мерен вектор от единици. Да се опитаме да проверим наличието на линейна връзка между X и y.

Нека е вярна хипотезата Ho: a = 0. Естествената контра хипотеза е H1: a № 0. Следователно, Z0 има размерност k = 1, а Z1 е с размерност m = dim(a)+1. От теорема 8.2 получаваме, че критичната област за проверка на хипотезата H0: z О Z0 срещу хипотезата H1:z О Z1\Z0 се определя от неравенството:

F = ||y1-y0||2/(m-1)
||y-y1||2/(n-m)
 > F1-a,
като при изпълнена H0 статистиката F О F(m-1,n-m).

В приложната статистика съответните суми от квадрати имат популярни наименования, разкриващи тяхната роля в тази проверка:

SSR = ||y-y1||2 = n
е
 i = 1 
 (yi - ^
y
 
i 
 )2       - Sum of Squares of Residuals

SSM = ||y1-y0||2 = n
е
 i = 1 
 ( ^
y
 
i 
 - _
y
 
 )2       - Sum of Squares due to the Model

Частното

R2 = SSM
SSM+SSR
се нарича коефициент на детерминация и има смисъла на коефициент на корелация - колкото по - близко е до единицата, толкова по ''детерминиран'' е моделът.

9.2  Проверка за равенство на нула на някой от коефициентите

Нека е вярна хипотезата H0: a1 = 0. Естествената контра хипотеза е H1: a1 № 0. Следователно, Z0 има размерност k = dim(a)-1 , а Z1 - размерност m = dim(a). От теорема 8.2 получаваме, че оптималната критична област за проверка H0: z О Z0 срещу хипотезата H1:z О Z1\Z0 се определя от неравенството:

F = ||y1-y0||2
||y-y1||2/(n-m)
 > F1-a,
като при изпълнена H0 статистиката F О F(1,n-m). Но това е квадрат на t-разпределение, от където получаваме, че статистиките
ti =
Ц(n-m) ^
a
 
i 
^
s
 
 2
 
 ((XўX)-1ii)1/2
(9.2)
имат разпределение на Стюдент с n-m степени на свобода при изпълнена хипотеза H0:ai = 0. Естествено, със съшото разпределение се пресмятат и доверителните интервали около оценките за неизвестните параметри (при изпълнена H1). Това следва от неизместеността им и от това, че оценките на параметрите не зависят от оценката на дисперсията.

Изведете строго разпределението на статистиките (9.2).

9.3  Доверителен интервал за прогноза

За произволни стойности x на предикторите от областта, за която е верен модела (9.1), случайната величина [^(y)] = xў[^(a)]+[^(b)] е неизместена оценка за E (y | x) и

D ( ^
y
 
 |x) = s2( 1
n
 +(x - _
X
 
 )ў( ~
X
 
 ў ~
X
 
 )-1(x - _
X
 
 )).
(9.3)

Тук с [`(X)] сме означили вектора 1/nXўE и E е (n xm) матрица от единици, а с [(X)\tilde] сме означили матрицата от центрирани данни (с извадена средна стойност). Следователно, грешката на прогнозираната стойност на конкретното наблюдение ще бъде

sy2(x) = s2(1 + 1
n
 + (x - _
X
 
 )ў( ~
X
 
 ў ~
X
 
 )-1 (x - _
X
 
 )).
(9.4)
Проверете уравнения (9.3) и (9.4).

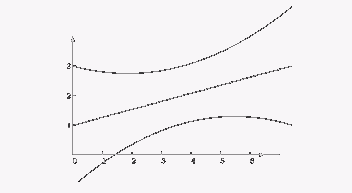
confregr.gif
Фигура 9.1: Проста линейна регресия

На фигурата е нарисувана апроксимиращата права при простия линеен модел y = ax+b+e. С двете параболи са отбелязани доверителните граници за наблюдаваната стойност съгласно формула (9.4). С аналогична форма, но значително по - тесен е коридорът за модела - формула (9.3). Така се вижда колко опасни (и понякога безсмислени) могат да бъдат прогнози за далечното бъдеще, основани на тенденция, наблюдавана в краен интервал от време.

9.4  Проверка на адекватността на модела

Проверката за адекватност на модела в регресионния анализ е възможна само в два случая: ако е известна s2 или ако разполагаме с независима от SSR и от параметрите на модела нейна оценка.

В първия случай можем да пресметнем статистиката SSR, която има разпределение s2c2 със степени на свобода n-m, ако моделът е адекватен, и отместено надясно разпределение при неадекватен модел. Така проверката е лесна - критичната област се определя от неравенството:

SSR > s2 c21-a.

Във втория случай, когато не знаем s2, се налага да използуваме някоя нейна оценка.

Най-популярния начин за получаване на независима оценка за s2 е да се провеждат повторни наблюдения при фиксирани стойности на предикторите. При такива наблюдения сумата SSR също се разлага на две независими събираеми, от които се конструира статистика, която има разпределение на Фишер, в случай че моделът е адекватен. Обикновено тази задача се решава със средствата на еднофакторния дисперсионен анализ. Отделните експериментални точки x се разглеждат като нива на фактор (групираща променлива). За всяко x имаме по nx наблюдения yi(x). Имаме равенството:

SSR =
е
 x 
 (yi(x)- _
y
 
 (x))2+
е
 x 
 nx ( _
y
 
 (x)- ^
y
 
 (x))2 = SSI + SSM.
(9.5)
Първата сума не зависи от модела, а втората има разпределение s2c2 със съответен брой степени на свобода, ако моделът е адекватен, и отместено надясно разпределение при неадекватен модел. Така критичната област ще се определи от неравенството:

SSM/k
SSI/j
 > F1-a,       j = n-m-k, k =
е
 x 
 (nx-1).

Опишете подпространствата Z0 и Z1 в този случай и изведете уравнение (9.5). Постройте критичната област.



Начало на лекцията | Съдържание | Индекс

File translated from TEX by TTH, version 2.10.
On 5 Apr 1999, 17:47.