Тема 1 Аксиоматика на теория на вероятностите

В тази лекция си поставяме следните цели:

да разгледаме генезиса на понятието вероятност;
да въведем събития и действия с тях;
да определим вероятностно пространство;
да дадем примери за прости вероятностни пространства.

1.1 Емпирични основи

Историята ни учи, че основите на понятието ''шанс'' са твърде стари. Това, което хората първо са забелязали, е устойчивостта на средната аритметична с нарастването на броя наблюдения. В миналото например, мерките за дължина са се определяли с ''усреднявяне''. В Англия, една от популярните мерки за дължина се е определяла като средна дължина на ходилото на първите 30 човека излизащи от черквата в неделя сутринта, в древния Египет - като общата дължина на определен брой семена от свещенно растение.

Честотна вероятност

Пример 1.1 Хвърляме монета многократно. Каква е честотата на получените ези?

Нека означим общия брой хвърляния с n, а броят на получените ези с m. Тогава честотата m/n на поява на ези би трябвало да клони към едно постоянно число:

Честотна вероятност

lim

Брой на благоприятните изходи

Брой на извършените опити

(1.1)

Така, ако монетата е правилна и хвърляме честно, би трябвало броят на езитата разделен на броя на опитите да клони към половина. Ако монетата не е правилна, граничната вероятност ще се окаже друго число, което е естествено да интерпретираме като оценка на шанса при един опит да получим ези.

Класическа вероятност

Първите опити да се построи математически модел са свързани с понятието равен ''шанс''. Предполага се, че даден опит има краен брой изходи, които са равноправни. При провеждане на опита се случва някой от тези изходи, при това всеки от тях може да се случи с еднакъв ''шанс''. Най-простите примери за такава концепция са свързани с хазартните игри, където се хвърлят зарове или използуват добре разбъркани тестета карти.

Пример 1.2 Хвърляме зар. Каква е вероятността да получим четно число?

Рецептата е проста. Достатъчно е да преброим благоприятните изходи и разделим това число с броя на всички изходи:

Класическа вероятност=

Брой на благоприятните изходи

Брой на всички възможни изходи

(1.2)

Така за нашата задача отговорът трябва да бъде 3/6=1/2.

Геометрична вероятност

Пример 1.3 (Задача на Бюфон) Хвърляме игла върху раирана покривка. Каква е вероятността иглата да пресече раето?

За да решим задачата трябва да формализираме условията. Нека означим с l дължината на иглата и с a - разстоянието между райетата. За простота ще сметнем, че широчината на едно райе е 0. Да означим с x разстоянието от средата на иглата до по - близкото райе,а с f - острия ъгъл, които иглата сключва с перпендикуляра към съшото райе.

Фигура 1.1: Иглата на Бюфон 1

Тогава имаме 0Ј x Ј a/2 и 0ЈfЈp/2. Това са всички възможности. Благоприятните (когато иглата пресече райето) се определят от неравенството: (l/2)cos f > x. Рецептата е проста:

Геометрична вероятност=

Площ на благоприятните изходи

Обща площ

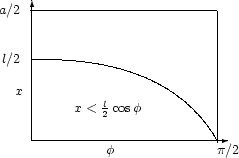Така, ако l<a, задачата се свежда до пресмятането на интеграла

p =

2 l

a p

у
х

cosa da =

2 l

a p

Фигура 1.2: Иглата на Бюфон 2

1.2 Аксиоматика

Теория на вероятностите става строга математическа теория едва след въвеждането в 1939 г. от А.Н.Колмогоров на следната аксиоматика, основана на теория на мярката (теория на интеграла).

Алгебра на събитията

Елементарно събитие е първично понятие -- нещо като точка в геометрията. Множеството от всички елементарни събития наричаме ''достоверно събитие'' и означаваме с W. Празното множество бележим с

и наричаме ''невъзможно събитие''.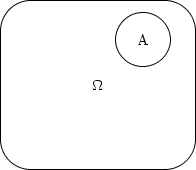

Всички събития са подмножества на W и с тях могат да се правят обичайните в теория на множествата действия. В теория на вероятностите събитието A има смисъла на логическото твърдение сбъднало се е някое от елементарните събития в A. Със събитията могат да се правят обичайните за множествата действия:допълнение, обединение, сечение, които обаче носят други имена.

Фигура 1.3: A в W

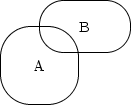Допълнението W\ A на множеството A в W означаваме с A и наричаме допълнително събитие (или отрицание) на събитието A.

Сечението на множествата A,B означаваме с AЗ B и казваме, че са се сбъднали съвместно събитията A и B.
Обединението на множествата A,B означаваме с AИ B и казваме, че се е сбъднало поне едно от събитията A и B. За краткост това се произнася сбъднало се е A или B.

Фигура 1.4: A и/или B

Когато AМ B казваме, че събитието A ''влече'' събитието B.

Операциите със събития удовлетворяват обичайните свойства на операциите с множества. Те лесно се разпространяват и върху безкраен брой събития. Изпълнени са и т.н. закони на Де Морган:

И_k A_k

З_k

A_k

З_k A_k

И_k

A_k

(1.3)

За удобство са въведени и някои производни определения и операции:

означаваме с A B = AЗ B;
събитията A и B наричаме несъвместими, ако A B=;
за несъвместими събития вместо AИ B използуваме знака събиране - пишем A+B;
означаваме с A D B = AB+AB.

За да си осигурим възможността да правим всичките тези операции ще поискаме множеството от събития да го допуска.

Определение 1.1 Семейство A от подмножества на W се нарича булова алгебра, ако удовлетворява следните три условия:

W О A;
ако AО A,то AО A;
ако A,B О A,то AИ BО A.

Веднага се вижда от 1.3, че буловата алгебра от множества е затворена и относно операциите З,D,+. Тя обаче не е длъжна да бъде затворена относно операции с безкраен брой множества.

Определение 1.2 Булова алгебра A, която е затворена относно изброимите операции обединение и сечение, се нарича булова s-алгебра -- ако A_kО A (k=1,2,...), то И_k A_kО A и З_k A_kО A.

Определение 1.3 Двойката (W, A), където A е булова s-алгебра, се нарича измеримо пространство. Елементите на A се наричат случайни събития.

s-алгебрите притежават някои универсални свойства. Например, сечение на произволен брой s-алгебри е s-алгебра. Това ни дава възможност да определим лесно минималната s-алгебра съдържаща семейството множества F като сечение на всички s-алгебри, съдържащи семейството F. Ще означаваме тази s-алгебра s( F).

Вероятностно пространство

Определение 1.4 Реалната функция P , определена върху елементите на буловата s-алгебра A, се нарича вероятност, ако удовлетворява условията:

неотрицателност: P (A)і 0," AО A;
нормираност: P (W)=1;
адитивност: Ако A_i З A_j = , то P (A₁+A₂+...)=P (A₁)+P (A₂)+.....

Определение 1.5 Тройката (W, A,P ) наричаме вероятностно пространство.

От аксиомите 1.4 лесно следват следните свойства на случайните събития.

P ()=0;
P (A)=1-P (A);
непрекъснатост в . Ако A_i, i=1,2,... е намаляваща редица от събития, т.е. A_i+1 М A_i и З_i A_i = , то lim_i P (A_i) = 0.

Да се върнем към примерите. Във пример 1.2 W се състои от 6 елемента, A е множеството от всички подмножества на това крайно множество. Вероятността се определя просто -- всички елементарни събития са равновероятни.

Значително по сложна е ситуацията при примера 1.3. Тук ролята на W се поема от множеството от всички точки (a,x) в правоъгълника 0ЈaЈp/2 и 0Ј x Ј a/2. s-алгебрата A се състои от измеримите по Лебег подмножества на този правоъгълник, т.е. тези на които можем да мерим лице или площ. Вероятността е относителната площ, заемана от тях в правоъгълника. Елементарните събития в това пространство притежават нулева вероятност.

Понякога се случва елементарните събития да не са събития, т.е. да не са елементи на A. За да избегнем тази и други неприятности обикновено попълваме A добавяйки към нея всички подмножества на събития с нулева вероятност. Ако означим това семейство от множества с N(P ), то прието е вместо с A да се работи с попълнената s-алгебра s( A, N(P )). Разбира се, такова попълнение зависи от вероятността P . От тук нататък, когато вероятността във вероятностното пространство е фиксирана, ще предполагаме, че A=s( A, N(P )).

Със задачата за монетата (пример 1.1) ще се заемем подробно в специална лекция. Тук само ще конструираме едно възможно пространство от елементарни събития за нея. Ако записваме резултата от един експеримент с число -- нула при получаване на тура и единица -- при получаване на ези, получаваме W като множеството от всички безкрайни двоични редици. (Предполагаме, че хвърляме неограничен брой пъти).

Ще докажем една лема, която има самостоятелно значение.

Лема 1.1 Нека вероятността P е зададена върху буловата алгебра F и е адитивна. Тогава, необходимо и достатъчно условие да е непрекъсната в

, е тя да е s-адитивна върху F.

Доказателство: Необходимост. Нека A=S_n=1^ҐA_n и A, A_nО F. От адитивността на P за " n следва равенството

P (A) = P (A₁)+P (A₂)+...+P (A_n)+ P

(

i=n+1

A_i). (1.4)

От непрекъснатостта следва, че P (S_i=n+1^ҐA_i)

0. Следователно, P е s-адитивна върху F.

Достатъчност. Нека B_n+1 М B_n О F и З B_n=

. Да положим A_n= B_n \ B_n+1. Тъй като " n, B_n=S_i=n^ҐA_i и P е s-адитивна върху F, получаваме, че

(B_n) =

i=n

P ( A_i) ѕ® 0

като остатък на сходящ се ред. Значи P е непрекъсната.

Пример 1.4 Вероятност, която не е непрекъсната в

Да разгледаме множеството W= (0,.5]. Върху всички отворени отляво и затворени отдясно интервали ( 0Ј aЈ bЈ .5) определяме вероятността така:

P ((a,b])=

м
н
о

b-a,	a>0
.5+b,	a=0

Множеството от крайните обединения на такива интервали F е буловата алгебра. Проверете го. Проверете, че P е зададена коректно, но не е непрекъсната в

1.3 ^*Теорема за продължението

Следната знаменита теорема се нарича теорема за продължение на вероятности върху s-алгебра.

Теорема 1.1 Ако една вероятност, зададена върху буловата алгебра, е непрекъсната в

, то тя е продължима еднозначно върху s( F).

Доказателство: Виж в приложението.

Граница на редица събития

В буловата s-алгебра A сме в състояние да въведем граница на събития и така, че тя да се окаже събитие. Означаваме:

A^* =

limsup

A_n= З

n=1

k=n

A_k , A_* =

liminf

A_n= И

n=1

k=n

A_k (1.5)

Интерпретацията на така определените гранични събития е следната:

A^* - се състои от тези елементарни събития, които влекат безкраен брой елементи A_n;
A_* - се състои от тези елементарни събития, които влекат всички елементи A_n от дадено място нататък;

Наистина, wО A^* може да се интерпретира така: " n $ k>n такова, че wО A_k. Аналогично, wО A_* може да се интерпретира така: $ n " k>n такова, че wО A_k. Очевидно при това A_*М A^* .

Метрично пространство на събитията

Нека определим за всеки две събития от една алгебра F числото r(A,B) = P (AD B). Лесно се проверява, че то е неотрицателно и удовлетворява неравенството на триъгълника. От никъде, обаче не следва, че ако r(A,B)=0, то A=B, както това става в крайно вероятностно пространство с класическа вероятност.

Нека r(A,B) е определено на s-алгебра с s-адитивна вероятност. Проверете, че сходимостта с това разстояние е еквивалентна на условието: P (A^*\ A_*)=r(A^*,A_*)=0.

За да може r(A,B) да стане разстояние (или метрика) е необходимо да разгледаме множеството от класове еквивалентни събития A^~, (казваме че A~ B, ако r(A,B) = 0). Това множество е също s-алгебра, но освен това става (компактно) метрично пространство (зависещо от вероятността P ).

Д.Въндев -Теория на вероятностите - January 9, 2002

Тема 1 Аксиоматика на теория на вероятностите

1.1 Емпирични основи

Честотна вероятност

Класическа вероятност

Геометрична вероятност

1.2 Аксиоматика

Алгебра на събитията

Вероятностно пространство

1.3 *Теорема за продължението

Граница на редица събития

Метрично пространство на събитията

1.3 ^*Теорема за продължението