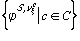 =min
=min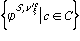 =("xj)S,vў,
=("xj)S,vў,| Previous | Next | Contents |
От тази дефиниция могат да се извлекат следните заключения:
а) атомарните формули нямат свързани променливи;
б) ако j е формула, то една променлива е свързана променлива на Шj точно
тогава, когато е свързана променлива на j;
в) ако j1 и j2 са формули, а g е двувалентен логически знак, то една променлива
е свързана променлива на (j1gj2) точно тогава, когато е свързана променлива на j1 или е свързана променлива на j2;
г) ако j е формула, h е променлива и k е някой от кванторите "h и $h, то една променлива е свързана променлива на kj точно тогава, когато съвпада с h или е свързана променлива на j.
Горните твърдения позволяват да се докаже по индукция, че за всяка дадена формула множеството на нейните свързани променливи е крайно.
Със следващата дефиниция, която ще дадем, ще въведем понятието свободна променлива, при това ще го въведем и за термове, и за формули. Дефиницията е пак индуктивна. Състои се от следните точки, където x е произволна променлива:
СВО1. x е свободна променлива на x.
СВО2. Ако s принадлежи на WnИPn, където n>0, t1, ..., tn са термове и x е свободна променлива на поне един от тези термове, то x е свободна променлива
на s(t1,...,tn).
СВО3. Ако x е свободна променлива на дадена формула j, то x е свободна променлива и на Шj.
СВО4,5. Ако x е свободна променлива на някоя от формулите j1 и j2, то x е
свободна променлива на (j1&j2) и x е свободна променлива на (j1Ъj2).
СВО6,7. Ако x е свободна променлива на дадена формула j, а h е променлива, различна от x, то x е свободна променлива на "hj и x е свободна променлива на $hj.
Винаги, когато q е терм или формула, ние ще означаваме със СВО(q) множеството на свободните променливи на q. От дадената по-горе индуктивна дефиниция се получават следните заключения:
а) за всяка променлива x е в сила равенството СВО(x)={x};
б) ако l принадлежи на W0ИP0, то СВО(l)=Ж;
в) ако l принадлежи на WnИPn, където n>0, а t1, ..., tn са термове, то
| СВО(l(t1,...,tn)) = | ою i=1 | СВО(ti); |
От тези твърдения следва разбира се, че за всеки терм и за всяка формула съответното множество на свободните променливи е крайно. При формулите няма никаква задължителна връзка между множеството на свързаните и множеството на свободните променливи;1 все пак понякога ще предпочитаме да работим с такива формули, на които множеството на свободните променливи няма общи елементи с множеството на свързаните променливи.
С индукция, съобразена с дефиницията на понятието затворен терм, се показва, че затворените термове нямат свободни променливи, а с индукция, съобразена с дефиницията на понятието терм, се доказва, че всеки терм е затворен или има поне една свободна променлива. Оттук се получава, че един терм е затворен точно тогава, когато той няма свободни променливи. Същото веднага се пренася и за атомарни формули: една атомарна формула е затворена точно тогава, когато тя няма свободни променливи. Това ни дава повод за следната обща дефиниция: една формула ще наричаме затворена, ако тази формула няма свободни променливи.
Пример. Ако p е едноместен предикатен символ, а x е променлива, то формулите "xp(x) и $xp(x) са затворени, макар че при тяхното построяване е използвана променливата x (тя е тяхна свързана променлива).
В нашите разглеждания понятието свободна променлива ще играе значителна роля благодарение на следното твърдение, което ще докажем:
Лема за базисна роля на свободните променливи. Нека S е дадена структура. Тогава всеки път, когато m е терм или формула, а v и vў са две оценки, които съвпадат върху свободните променливи на m,2 в сила е равенството
 и
и 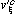 съвпадат върху свободните променливи на формулата j, защото коя да е свободна променлива на j съвпада с x или е свободна променлива на "xj. Оттук виждаме, че
съвпадат върху свободните променливи на формулата j, защото коя да е свободна променлива на j съвпада с x или е свободна променлива на "xj. Оттук виждаме, че
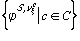 =min
=min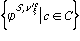 =("xj)S,vў,
=("xj)S,vў,Следствие. Ако m е затворен терм или затворена формула, то mS,v=mS,vў за всеки две оценки v и vў в S на променливите.
Горното следствие показва, че когато m е затворен терм или затворена формула,
стойността mS,v не зависи от избора на оценката v в S на променливите. В
случая, когато m е затворен терм, това следва и от известното ни равенство
mS,v=mS, което е налице в този случай. Вземайки повод от верността на това равенство за произволен затворен терм m, осигуряваме неговата вярност и в
случая, когато m е затворена формула, като се уславяме независещата от избора на v стойност mS,v да означаваме с mS; тази независеща от избора на v стойност ще наричаме стойност на m в S. Ако m е затворена формула, то при mS=1 ще казваме, че m е вярна в S, а при mS=0 ще казваме, че m е невярна в S. Очевидно
верността на една затворена формула в S е равносилна с нейната тъждествена вярност в S. Поради това факта, че дадена затворена формула m е вярна в S, можем да запишем, като пишем S j; разбира се отрицанието на този факт, т.е.
неверността на j в S, можем да запишем, като пишем S
j; разбира се отрицанието на този факт, т.е.
неверността на j в S, можем да запишем, като пишем S j.
j.
За произволна формула j, на която свободните променливи са x1, x2, ..., xn, формулата "x1"x2..."xnj очевидно е затворена (затворена формула от този вид ще наричаме затваряне на j). Следствието от лемата за запазване на тъждествената вярност при поставяне или премахване на квантор за общност показва, че споменатата затворена формула е вярна в дадена структура точно тогава, когато формулата j е тъждествено вярна в същата структура.
Бележки
1 Лесно може да се види, че ако Pn№Ж поне за едно n, различно от 0, то съществува
формула, на която множеството на свързаните променливи и множеството
на свободните променливи са произволни отнапред избрани крайни множества от
променливи.
2 Последното условие се счита изпълнено и в случая, когато m няма свободни променливи.
Последно изменение: 9.01.2001 г.
Previous
|
Next
|
Contents
| |