ФОРМУЛИ НА ПРЕДИКАТНОТО СМЯТАНЕ
Някои думи над азбуката A, разширена със знаците "(", ")", "[", "]", "<", ">", ",", "Ш", "&" и "Ъ", ще наричаме формули. Дефиницията е индуктивна:
Ф1. Всяка атомарна формула е формула.
Ф2. Ако j е формула, то думата Шj също е формула (нарича се отрицание
на j и се чете "не j").
Ф3. Ако j1 и j2 са формули, то думaтa (j1&j2) също е формула (нарича се конюнкция на j1 и j2 и се чете "j1 и j2").
Ф4. Ако j1 и j2 са формули, то думaтa (j1Ъj2) също е формула (нарича се дизюнкция на j1 и j2 и се чете "j1 или j2").
Ф5. Ако j е формула, а x е дума от X, то думата [x]j също е формула (нарича се x-генерализация на j и се чете "за всяко x j"; думата [x] се нарича квантор за общност относно x и се означава с "x).
Ф6. Ако j е формула, а x е дума от X, то думата <x>j също е формула
(нарича се x-екзистенциализация на j и се чете "за някое x j"; думата <x>
се нарича квантор за съществуване относно x и се означава с $x).
Забележка. Използването на думи от вида [x] и <x> в качеството на квантори за общност и за съществуване е нетрадиционно, но то е в съзвучие с означенията в съвременни направления на тъй наречената модална логика, изучаващи повече от един вид необходимост и възможност.
Лесно се вижда, че никоя формула не е същевременно терм - за атомарните формули това вече го установихме, а за останалите следва от обстоятелството, че всяка от тях съдържа някой от знаците за отрицание, за конюнкция или за дизюнкция или пък квадратни или ъглови скоби - знаци, които не участват в никой терм.
Ще покажем, че и при формулите е налице еднозначност на синтактичния анализ - всяка формула се получава само по една от точките Ф1-Ф6 на дефиницията и само по един начин. За целта първо отбелязваме, че формулите, получени по точка Ф1, не могат да се получат по никоя от останалите пет точки, тъй като не съдържат никой от изброените преди малко няколко знаци. От друга страна първите букви на формулите, получени по различни измежду точките Ф2-Ф6, са винаги различни освен в случая, когато едната формула е получена по точка Ф3, а другата - по точка Ф4. Следователно, ако изключим последния случай, то можем да твърдим, че формули, получени по различни измежду точките Ф2-Ф6, не могат да
съвпадат. За да покажем, че не могат да съвпадат и формули, получени по точка Ф3 и точка Ф4, ще си послужим със следните леми, на които доказателството е с индукция, съобразена с индуктивната дефиниция на понятието формула.
Лема 1. Във всяка формула броят на участията на лява кръгла скоба е равен на броя на участията на дясна кръгла скоба.
Лема 2. Във всяко начало на формула, завършващо със знак за конюнкция или знак за дизюнкция, броят на участията на лява кръгла скоба е по-голям от броя на участията на дясна кръгла скоба.
Като разполагаме с тези леми, да предположим, че за някои формули j1, j2,
j1ў, j2ў, имаме равенство от вида (j1gj2)=(j1ўgўj2ў), където и g, и gў е знак за
конюнкция или знак за дизюнкция. Ще покажем, че в такъв случай имаме равенствата
j1=j1ў, g=gў, j2=j2ў. За тази цел е достатъчно да отбележим, че от предположеното равенство следва разбира се равенството j1gj2=j1ўgўj2ў, а от
него пък и от изказаните преди малко две леми е ясно, че думите j1 и j1ў трябва
да имат равни дължини.
Току-що установеният факт показва не само това, че не може една формула да бъде получена и по точка Ф3, и по точка Ф4. Той показва още, че когато една формула е получена по някоя от тези две точки, то тя може да бъде получена по нея само по един начин. Последното обаче е очевидно вярно и за всяка от останалите точки от дефиницията. С това еднозначността на синтактичния анализ на формулите е доказана.
Еднозначността на синтактичния анализ на формулите ни позволява в частност да използваме следната терминология: ако j1 и j2 са формули, а j е тяхната конюнкция или тяхната дизюнкция, то формулите j1 и j2 ще наичаме съответно пръв член и втори член на j .
Сега ще искаме да дефинираме кога една формула е вярна в дадена структура
S=(C,I) при дадена оценка в S на променливите. Преди това ще дадем една друга
дефиниция, имаща отношение към въпроса. В нея ще използваме означенията min B
и max
B
и max B съответно за най-малкото и най-голямото число в дадено непразно крайно множество от числа B, както и следното означение: ако v е оценка в S на променливите, x е променлива и c е даден елемент на C, то
B съответно за най-малкото и най-голямото число в дадено непразно крайно множество от числа B, както и следното означение: ако v е оценка в S на променливите, x е променлива и c е даден елемент на C, то  е оценката в S на променливите, която приема стойност c за променливата x, а за всички останали променливи съвпада с v (тази оценка ще наричаме x,c-модификация на v). С дефиницията, която сега ще дадем, ще определим индуктивно кога една формула има в S при дадена оценка на променливите дадена стойност, принадлежаща на
множеството {0,1}. Дефиницията се състои от следните приемания, в които v е произволна оценка в S на променливите, x е произволна променлива, а допустимите
стойности на b, b1, b2 са 0 и 1:
е оценката в S на променливите, която приема стойност c за променливата x, а за всички останали променливи съвпада с v (тази оценка ще наричаме x,c-модификация на v). С дефиницията, която сега ще дадем, ще определим индуктивно кога една формула има в S при дадена оценка на променливите дадена стойност, принадлежаща на
множеството {0,1}. Дефиницията се състои от следните приемания, в които v е произволна оценка в S на променливите, x е произволна променлива, а допустимите
стойности на b, b1, b2 са 0 и 1:
СФ1. Ако a е атомарна формула, то a има стойност aS,v в S при оценката v.
СФ2. Ако дадена формула j има стойност b в S при оценката v, то формулата
Шj има стойност 1-b в S при оценката v.
СФ3. Ако дадени формули j1 и j2 имат съответно стойности b1 и b2 в S при
оценката v, то формулата (j1&j2) има стоиност min{b1,b2} в S при оценката v.
СФ4. Ако дадени формули j1 и j2 имат съответно стойности b1 и b2 в S при
оценката v, то формулата (j1Ъj2) има стоиност max{b1,b2} в S при оценката v.
СФ5. Ако при всеки избор на елемента c на C дадена формула j има стойност
1 в S при оценката  , то формулата "xj има стойност 1 в S при оценката v.
, то формулата "xj има стойност 1 в S при оценката v.
СФ5ў. Ако при някой избор на елемента c на C дадена формула j има стойност
0 в S при оценката  , то формулата "xj има стойност 0 в S при оценката v.
, то формулата "xj има стойност 0 в S при оценката v.
СФ6. Ако при някой избор на елемента c на C дадена формула j има стойност
1 в S при оценката  , то формулата $xj има стойност 1 в S при оценката v.
, то формулата $xj има стойност 1 в S при оценката v.
СФ6ў. Ако при всеки избор на елемента c на C дадена формула j има стойност
0 в S при оценка  , то формулата $xj има стойност 0 в S при оценка v.
, то формулата $xj има стойност 0 в S при оценка v.
Можем да считаме, че в рамките на горната дефиниция структурата S остава фиксирана и дефиницията действа в множеството на всички наредени тройки (j,v,b), където j е формула, v е оценка в S на променливите, b е елемент на множеството {0,1}, а също, че с тази дефиниция се определя за кои тройки (j,v,b) от въпросното множество приемаме, че b е стойност на j в S при оценка v. При такава гледна точка дефиницията може да се представи чрез индуктивен механизъм в споменатото множество, състоящ се от индукторите от следните видове, където v може да бъде произволна оценка в S на променливите (разбира се тези видове съответстват на отделните приемания от дефиницията):
Вид 1: Ж/(a,v,aS,v), където a е атомарна формула.
Вид 2: {(j,v,b)}/(Шj,v,1-b), където j е формула, а b е число от множеството {0,1}.
Вид 3,4: {(j1,v,b1),(j2,v,b2)}/((j1&j2),v,min{b1,b2}) или {(j1,v,b1),(j2,v,b2)}/((j1Ъj2),v,max{b1,b2}), където j1 и j2 са формули, а b1 и b2 са числа от множеството {0,1}.
Вид 5,6ў: {(j, ,1)|cОC}/("xj,v,1) или {(j,
,1)|cОC}/("xj,v,1) или {(j, ,0)|cОC}/($xj,v,0), където j
е формула, а x е променлива.
,0)|cОC}/($xj,v,0), където j
е формула, а x е променлива.
Вид 5ў,6: {(j, ,0)}/("xj,v,0) или {(j,
,0)}/("xj,v,0) или {(j, ,1)}/($xj,v,1), където j е формула, x е променлива, c е елемент на C.
,1)}/($xj,v,1), където j е формула, x е променлива, c е елемент на C.
Забележка. В случаите, когато множеството C е безкрайно, посоченият индуктивен механизъм не е финитарен.
Това е така, защото в тези случаи предпоставките
на индукторите от вид 5,6ў са безкрайни множества.
Ще покажем, че при произволно избрана оценка v в S на променливите всяка
формула има точно една стойност в S при оценка v. Това ще го докажем чрез индукция,
съобразена с индуктивната дефиниция на понятието формула; в разсъжденията
ще използваме установената преди малко еднозначност на синтактичния анализ
на формулите.
Ако една формула a е атомарна, то точка СФ1 й предписва в S при оценка v
стойността aS,v и само нея, а никоя от останалите точки не предписва стойност
на a, защото в тях се предписват стойности само на неатомарни формули.
Ако дадена формула j има единствена стойност b в S при оценка v, то точка
СФ2 предписва на формулата Шj в S при оценка v стойността 1-b и само нея (поради
еднозначното представяне на формулата Шj в този вид), а никоя от останалите
точки не предписва стойност на Шj, защото формулите, разглеждани в тях,
са различни от Шj.
Ако дадени формули j1 и j2 имат съответно единствени стойности b1 и b2 в S
при оценка v, то точка СФ3 предписва на формулата (j1&j2) в S при оценка v
стойността min{b1,b2} и само нея (поради еднозначното представяне на формулата
(j1&j2) в този вид), а никоя от останалите точки не предписва стойност на
(j1&j2), защото формулите, разглеждани в тях, са различни от (j1&j2).
По напълно аналогичен начин се вижда, че и формулата (j1Ъj2) има точно една
стойност в S при оценка v, когато j1 и j2 имат единствени стойности в S при
оценка v.
Да предположим сега, че за всяка оценка в S на променливите дадена формула
j има единствена стойност в S при тази оценка. Ще покажем, че същото важи и за
формулите "xj и $xj, където x е произволна променлива. Ще се ограничим с разглеждането
на въпроса за първата от тези две формули, а за втората разсъжденията
са аналогични. Нека v е произволна оценка в S на променливите. Преди
всичко ясно е, че стойност на формулата "xj в S при оценка v биха могли да
предпишат само точки СФ5 и СФ5ў, като всяка от тях поотделно може да предпише
най-много една стойност на въпросната формула. Ако допуснем, че всяка от споменатите
точки предписва стойност на "xj, ще се получи, че за някое c от C
формулата j има в S при оценка  както стойност 1, така и стойност 0, а това
противоречи на направеното индуктивно предположение. Оттук е ясно, че формулата
"xj има най-много една стойност в S при оценка v. За да се убедим, че тази
формула има стойност в S при оценка v, ще отбележим, че е налице някой от следните
два случая: а) за всяко c от C единствената стойност на формулата j при
оценката
както стойност 1, така и стойност 0, а това
противоречи на направеното индуктивно предположение. Оттук е ясно, че формулата
"xj има най-много една стойност в S при оценка v. За да се убедим, че тази
формула има стойност в S при оценка v, ще отбележим, че е налице някой от следните
два случая: а) за всяко c от C единствената стойност на формулата j при
оценката  е 1; б) за някое c от C единствената стойност на j при оценката
е 1; б) за някое c от C единствената стойност на j при оценката  е различна от 1 и следователно е 0. В случая а) обаче формулата "xj ще има
стойност 1 в S при оценка v, а в случая б) - стойност 0.
е различна от 1 и следователно е 0. В случая а) обаче формулата "xj ще има
стойност 1 в S при оценка v, а в случая б) - стойност 0.
Обобщаваме означението за стойност на атомарна формула в конфигурация,
като се уславяме за всяка формула j и всяка оценка v в S на променливите
да означаваме с jS,v единствената стойност на j в S при оценка v. От точки
СФ2-СФ6ў на дефиницията за стойност на формула се получава, че при всеки избор
на формулите j, j1, j2, на променливата x и на оценката v в S са изпълнение
следните равенства:
(Шj)S,v=1-jS,v, (j1&j2)S,v=min{j1S,v,j2S,v}, (j1Ъj2)S,v=max{j1S,v,j2S,v},
("xj)S,v=min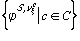 , ($xj)S,v=max
, ($xj)S,v=max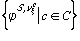 .
Ако за дадена формула j и дадена оценка v в S имаме равенството jS,v=1, то
ще казваме, че j е вярна в S при оценка v, и ще пишем S,v
.
Ако за дадена формула j и дадена оценка v в S имаме равенството jS,v=1, то
ще казваме, че j е вярна в S при оценка v, и ще пишем S,v j, а ако имаме
равенството jS,v=0, то ще казваме, че j е невярна в S при оценка v, и ще
пишем S,v
j, а ако имаме
равенството jS,v=0, то ще казваме, че j е невярна в S при оценка v, и ще
пишем S,v j. От написаните по-горе равенства се вижда, че при използваните в тях означения са в сила следните твърдения, където знакът "Ы" замества думите
"точно тогава, когато":
j. От написаните по-горе равенства се вижда, че при използваните в тях означения са в сила следните твърдения, където знакът "Ы" замества думите
"точно тогава, когато":
S,v Шj Ы S,v
Шj Ы S,v j,
S,v
j,
S,v (j1&j2) Ы S,v
(j1&j2) Ы S,v j1 и S,v
j1 и S,v j2,
S,v
j2,
S,v (j1Ъj2) Ы S,v
(j1Ъj2) Ы S,v j1 или S,v
j1 или S,v j2,
S,v
j2,
S,v "xj Ы S,
"xj Ы S,
 j за всяко c от C,
S,v
j за всяко c от C,
S,v $xj Ы S,
$xj Ы S,
 j за някое c от C.
j за някое c от C.
Ако една формула j е вярна в структурата S при всяка оценка в S на променливите,
то ще казваме, че j е тъждествено вярна в S и ще пишем S j. Когато
дадена формула j е тъждествено вярна във всяка структура, ще казваме, че j
е тъждествено вярна и ще пишем
j. Когато
дадена формула j е тъждествено вярна във всяка структура, ще казваме, че j
е тъждествено вярна и ще пишем  j.
j.
Пример. Нека p е едноместен предикатен символ, а x и y са две различни
променливи. Тогава формулата (p(x)ЪШp(y)) не е тъждествено вярна, но е тъждествено
вярна във всяка структура, на която носителят е едноелементно множество.
От друга страна, формулата (p(x)ЪШp(x)) е тъждествено вярна.
Следното твърдение ще бъде твърде полезно при някои по-нататъшни разглеждания.
Лема за запазване на тъждествената вярност при поставяне или премахване на квантор за общност. Нека j е формула, x е
променлива и S е структура. Тогава за да бъде формулата "xj тъждествено вярна в S, необходимо и достатъчно е формулата j да бъде тъждествено
вярна в S.
Доказателство. Нека S=(C,I). Изискването формулата "xj да бъде тъждествено вярна в S е изпълнено точно тогава, когато за всяка оценка v в S на променливите
и за всеки елемент c на C формулата j е вярна в S при оценка  . Това показва веднага, че ако j е тъждествено вярна в S, то "xj също е тъждествено вярна в S. Съвсем просто обаче се вижда, че и обратно, ако "xj е тъждествено вярна в S, то и j е тъждествено вярна в тази структура. За целта е достатъчно да се отбележи, че ако v е произволна оценка в S на променливите, то v=
. Това показва веднага, че ако j е тъждествено вярна в S, то "xj също е тъждествено вярна в S. Съвсем просто обаче се вижда, че и обратно, ако "xj е тъждествено вярна в S, то и j е тъждествено вярна в тази структура. За целта е достатъчно да се отбележи, че ако v е произволна оценка в S на променливите, то v= , където c=v(x).
, където c=v(x).
Следствие. Ако j е формула, x1, x2, ..., xn са променливи и S е структура, то формулата "x1"x2..."xnj е тъждествено вярна в S точно тогава, когато формулата j е тъждествено вярна в S.
Последно изменение: 26.07.1999 г.
 B
и max
B
и max B съответно за най-малкото и най-голямото число в дадено непразно крайно множество от числа B, както и следното означение: ако v е оценка в S на променливите, x е променлива и c е даден елемент на C, то
B съответно за най-малкото и най-голямото число в дадено непразно крайно множество от числа B, както и следното означение: ако v е оценка в S на променливите, x е променлива и c е даден елемент на C, то  е оценката в S на променливите, която приема стойност c за променливата x, а за всички останали променливи съвпада с v (тази оценка ще наричаме x,c-модификация на v). С дефиницията, която сега ще дадем, ще определим индуктивно кога една формула има в S при дадена оценка на променливите дадена стойност, принадлежаща на
множеството {0,1}. Дефиницията се състои от следните приемания, в които v е произволна оценка в S на променливите, x е произволна променлива, а допустимите
стойности на b, b1, b2 са 0 и 1:
е оценката в S на променливите, която приема стойност c за променливата x, а за всички останали променливи съвпада с v (тази оценка ще наричаме x,c-модификация на v). С дефиницията, която сега ще дадем, ще определим индуктивно кога една формула има в S при дадена оценка на променливите дадена стойност, принадлежаща на
множеството {0,1}. Дефиницията се състои от следните приемания, в които v е произволна оценка в S на променливите, x е произволна променлива, а допустимите
стойности на b, b1, b2 са 0 и 1: , то формулата "xj има стойност 1 в S при оценката v.
, то формулата "xj има стойност 1 в S при оценката v. , то формулата "xj има стойност 0 в S при оценката v.
, то формулата "xj има стойност 0 в S при оценката v. , то формулата $xj има стойност 1 в S при оценката v.
, то формулата $xj има стойност 1 в S при оценката v. , то формулата $xj има стойност 0 в S при оценка v.
, то формулата $xj има стойност 0 в S при оценка v.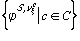 , ($xj)S,v=max
, ($xj)S,v=max j, а ако имаме
равенството jS,v=0, то ще казваме, че j е невярна в S при оценка v, и ще
пишем S,v
j, а ако имаме
равенството jS,v=0, то ще казваме, че j е невярна в S при оценка v, и ще
пишем S,v j. От написаните по-горе равенства се вижда, че при използваните в тях означения са в сила следните твърдения, където знакът "Ы" замества думите
"точно тогава, когато":
j. От написаните по-горе равенства се вижда, че при използваните в тях означения са в сила следните твърдения, където знакът "Ы" замества думите
"точно тогава, когато":