Лекция 13
Критерии за съгласие

• ще докажем теоремата на Гливенко - Кантели;
• ще опишем критерия на Колмогоров - Смирнов;
• ще опишем c² критерия за съгласие;
• ще дадем представа за някои методи за апроксимация на плътности.

13.1  Теорема на Гливенко-Кантели

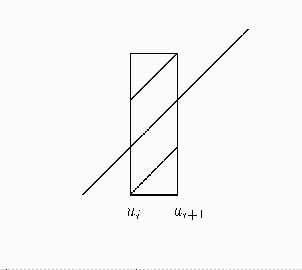
Имаме EF_n(x) = F(x),       D F_n(x) = F(x)(1-F(x))/n. Следователно, F_n(x) клони п.с. към теоретичната F(x) за всяко фиксирано x. Верно е обаче по - силното твърдение на Гливенко - Кантели:

Теорема 1

Доказателство:  Първо да отбележим, че без намаление на общността можем да считаме F(x) строго растяща функция. Ще докажем теоремата при допълнителното ограничение, че тя няма скокове - т.е. е непрекъсната. Тогава тя притежава обратна функция F^-1(u), определена на интервала (0,1).

Сега твърдението на теоремата може да се препише в следната форма:

Фигура 13.1: Един интервал

На фигура 13.1 е показан един такъв интервал. С удебелена линия е отбелязана ''целевата'' функция u. Границите на интервалите да означим с u_i = i/r. Тъй като във всяка от точките u_i G_n(u_i) клони п.с. към u_i, можем да подберем N така, че "n > N да е изпълнено неравенството:

Сега остава да отбележим, че G_n е монотонна, и ако в краищата на интервала |G_n(u_i) - u_i| Ј e, то вътре в интервала |G_n(u) - u| Ј 2e.

Така получаваме:

Така с помощта на тази теорема получаваме лесно силна състоятелност на много статистически оценки.

13.2  Критерий на Колмогоров - Смирнов

Една от основните задачи на статистиката е проверката на съответствие на теоретичното разпределение с извадката. Това е нещо като проверка на адекватността на модела - нашите предположения за разпределението. Следната теорема ни дава средства за това:

Теорема 2 (Колмогоров - Смирнов) За всяка непрекъсната функция на разпределение F(x) е в сила съотношението:

Доказателство: Виж например [Янев, Димитров (1990)].Q.E.D.

Функцията е K(x) табулирана и това прави използуването на критерия сравнително леко. От таблицата се извлича квантила k_a: K(k_a) = 1 - a за необходимото критично ниво a. От данните и теоретичната ф.р. F(x) се пресмята статистиката ЦnD_n и се сравнява с k_a. Ако я надхвърли, хипотезата за съгласие се отхвърля.

13.3  c²-критерий

Фигура 13.2: Една хистограма

Нека ни е зададена някаква теоретична плътност p(x) и имаме за задача да проверим съгласуваността й с извадката. Нека разполагаме с n наблюдения. Разделяме множеството от стойности на сл.в. (или носителя на плътността) на k интервала H_i, така че p_i = т_Hi p(x)dx > 0 и np_i > 5. Това изискване е важно. Понякога се налага някои интервали да се обединяват, за да може то да се удовлетвори. Съществува и вариант на хистограмата (и критерия), когато интервалите се избират равновероятни, т.е. p_i = p_j. Нека означим с n_i броя на наблюденията попаднали в H_i. Пресмятаме статистиката

Теорема 3 (Пирсън) Статистиката h има асимптотично (при n®Ґ) разпределение c² с k-1 степени на свобода.

Доказателство: Строгото доказателство е твърде трудоемко. Затова тук ще покажем само идеята. Всяко от събираемите в (13.2) представлява квадрата на центрирана асимптотично нормална сл.в. Действително, np_i = E n_i. За съжаление, тези величини са зависими - еn_i = n. Оказва се, че условното разпределение на сл. гаусов вектор x О N(0,I) в Rⁿ при условие (x, 1) = 0 е същото като асимптотичното съвместно разпределение на сл.в. n_i, съответно центрирани и нормирани. Q.E.D.

---

Начало на лекцията | Съдържание | Индекс