Понятието статистика е твърде широко. То включва в себе си както методи на просто преброяване и сгъстяване на информацията, така и методи за взимане на решения, основани на строги математически разсъждения. Да не говорим, че със същата дума ''статистика'' често означаваме и събраната информация - статистика зза футбола, например.
Основно понятие в статистиката е понятието ''генерална съвкупност''.
Определение 1 Генерална съвкупност наричаме множеството от обекти на изследване.
За едно изследване на ЦСИ това могат да бъдат:
За един орнитолог, който също използува методите на статистиката, това е популацията от щъркели, например. За преподавателя по статистика - това могат да бъдат студентите от неговия курс.
Наричаме изчерпателни данни данни, които напълно описват дадено явление. Такива са например данните получени при едно преброяване на населението в ЦСИ. За геолога, интересуващ се от съдържанието на желязо в Кремиковското находище, това ще е самото нахдище разделено на някакви малки обеми.
За съжаление такива данни рядко са достъпни, пък и струват прекалено скъпо. Когато не е възможно такова изследване и данните за интересуващото ни явление не са достъпни. Така че генералната съвкупност става абстрактно множество от обекти представляващо цел на нашето изследване.
В практиката често се работи с т.нар. извадка, част от генералната съвкупност. По този начин, търсените характеристики на генералната съвкупност се оценяват по данните от извадката.
Основна цел е по даден непълен обем данни да се направи някакво правдоподобно заключение за генералната съвкупност като цяло. Този набор от обекти, който всъщност се изследва (премерва, разпитва) се нарича извадка. Извадките биват систематични, случайни или подходящи за целите на изследването комбинации от двата метода.
Определение 2 Извадка наричаме подмножеството от обекти на генералната съвкупност, достъпно за премерване.
Например, една систематична извадка на дадено находище предполага сондажи разположени равномерно по площта му. От друга страна при случайната извадка се предполага, че шанса на всеки обект от генералната съвкупност да попадне в извадката е равен - всички обекти са равноправни и изборът е напълно случаен. Далеч не винаги е възможно да си избираме с кой от двата метода да конструираме извадката.
Това става с помощта на така наречения планиран (селскостопански) експеримент. Избираме няколко полета, засяваме ги с различни сортове пшеница и ги торим с различни видове тор. Така ще подберем подходящата за нашите цели комбинация (сорт и тор). Как обаче да избегнем влиянието на различните видове почва и може би природни условия? Как да намалим максимално броя на експериментслните полета за и без това скъпия и продължителен опит? На това ни учи планирането на експеримента. Математическа наука - част от математическата статистика.
Както се вижда, едва ли можем да гледаме на резултатите от такъв опит като на извадка от нещо.
Често нашите наблюдения са над някакво явление или процес, който се променя във времето. Това може да бъде курса на долара в поредни дни или средната температура на въздуха в София.
Наблюдението и тук не е извадка. Въпреки това, както ще видим по нататък, теорията на случайните процеси ни дава достатъчни математически средства да анализираме такива данни и правим (понякога разумни) прогози.
Информацията, която представляват данните обикновено се различава по това как се записва - понякога това са числа: размери, тегло, бройки и т.н. Друг път това са нечислови характеристики като цвят, форма, вид химическо вещество и т.н. Ясно е, че даже и да кодираме с числа подобни данни, при тяхното изучаване и представяне трябва да се отчита тяхната нечислова природа.
Представянето на данни всъщност е основна задача както на изчерпателната така и на извадъчната статистика. Информацията, която се съдържа в милионите числа трябва да бъде представена в обозрима форма, така че всеки да си представи основните качества на множеството обекти. Главна роля в това кондензиране на информация има графичното представяне. То е ефектно и в минимална степен при него се губи информация.
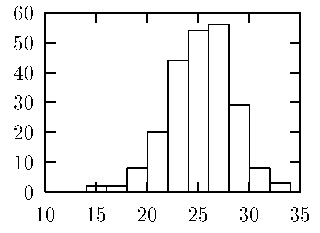
Хистограмата е основният вид за представяне на информацията за наблюдения върху числов признак. Тя се строи по просто правило. Избират се обикновено еднакво големи е не много на брой (5 - 20) еднакво големи прилежащи интервала покриващи множеството от стойности на наблюдавания признак. Те се нанасят върху оста x. След това всеки от обектите на извадката се премерва и получената стойност попада в някой от интервалите.

Ако интервалът [xmin, xmax] се раздели на k еднакви части с ширина h, т.е. h = [(xmax - xmin)/( k)] и за всяко h се преброят попаданията на стойностите, то полученото число n се нарича честота на срещане. Последната, нормирана спрямо общият брой на данните N, е известна като относителна честота на срещане fi = [(ni)/( N)], където с i е означен съответния интервал.
При графично маркиране на fi с помощта на стълбчета, с височина стойността на fi и ширина h, се получава хистограма, която служи за описание на изследваната съвкупност от данни (фиг.1.1).
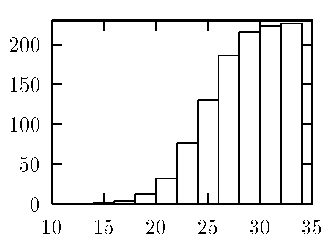
Също така много удобна е така наречената кумулативна
хистограма (фиг. 1.2).
Тя се строи по натрупаните данни и позволява
лесен отговор на въпроси от вида:
- каква е частта от наблюденията, попаднали под дадена
граница;
- кое е числото под което са половината наблюдения - т.н. медиана.
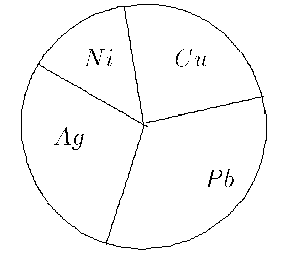
Когато изследваме нечислови признаци, най - подходящото представяне е като процентно съдържание, например на на гласовете поддени за различните партии в едно гласуване. Това може да се направи и с хистограма, но не е прието, тъй като разместването на стълбовете отговарящи на различните типове обекти променя общият вид на рисунката. Затова се използуват така наречените секторни диаграми или торти (piechart).
Отделните сектори отговарят по лице на пропорциите на различните типове и понякога са разноцветни.
Когато разгледаме нечислов признак на един случайно избран обект от генералната съвкупност, то той съгласно предположенията ни за равнопоставеност на обектите в извадката би трябвало да попадне в дадена категория с вероятност равна на пропорцията на обектите в тази категория от генералната съвкупност. Ако съвкупността е голяма (или извадката ни е с връщане), то броят на обектите от извадката ni с признак от категория i би трябвало да се окаже биномно разпределен с B(n,pi).
Определение 3 Наредените по големина стоиности на x1,x2,...,xn се наричат вариационен ред x(1) Ј x(2) Ј ј Ј x(n), а елементите на реда - порядкови статистики.
Така първата порядкова статистика x(1) = minI(xi), а последната x(n) = maxI(xi). Интуитивно е ясно, че информацията за генералната съвкупност, която се съдържа в извадката, е представена изцяло във вариационния ред. Същата информация може да се представи и в следната форма.
Определение 4
Извадъчна функция на разпределение наричаме функцията:
Fn(x) =
м
п
п
п
н
п
п
п
о
0
x < x(1)
k
n
x(k-1) Ј x < x(k)
1
x(n) Ј x
В приложната статистика често се използуват следните дескриптивни (описателни) статистики:
Те лесно се изразяват чрез извадъчната функция на разпределение:
|
|
Функциите mi наричаме извадъчни моменти. Извадъчните моменти mk са ''състоятелни'' оценки на моментите на сл.в. E xk. Същото твърдение важи и за други характеристики на извадъчното разпределение - квантили, медиана и т.н. Всички такива функции на извадъчното разпределение наричаме дескриптивни статистики. Например, порядковата статистика x(k) клони към квантила qa, ако k/n ® a.
Определение 5 Медиана се определя като решение на уравнението: F(m) = 1/2. Медиана на извадка (извадъчна медиана) е наблюдението, което разделя вариационния ред на две равни части (когато обемът е четен се взима средното на двете централни наблюдения).
Медианата описва положението на средата на разпределението върху числовата ос. В случая на големи отклонения от нормалност или при наличие на твърде отдалечени, съмнителни наблюдения, това е предпочитана оценка за ''средата'' на разпределението.
В много случаи се използува и положението на други характерни точки от разпределението.
Определение 6 Извадъчен квантил qa с ниво a на дадена извадка с ф.р. Fn се определя като приближено решение на уравнението: Fn(qa) = a.
Така медианата m = q1/2.
Обикновено тези методи се сумират под общото название анализ на данни.
В математическата статистика винаги се разглежда следния вероятностен модел. За всяко наблюдение се предполага, че то е сл.в. Ако наблюденията са много, то обикновено те са независими сл.в. Когато независимостта е съмнителна, се предполага някакво съвместно разпределение на тези сл.в. Въз основа на така направените предположения се изследват вероятностните свойства на различни ''полезни'' функции от наблюденията - техните разпределения, моменти и т.н.
Когато в тези функции се поставят реалните наблюдения, се получават конкретни стойности - числа. Въз основа на тези числа се правят заключения - статистически изводи - за самия модел. Идеята на тези изводи е, че при верен модел ние знаем доколко те са ''вероятни''.
Когато моделът се окаже неадекватен, се строи друг и т.н., както
изобщо в науката математическо моделиране.