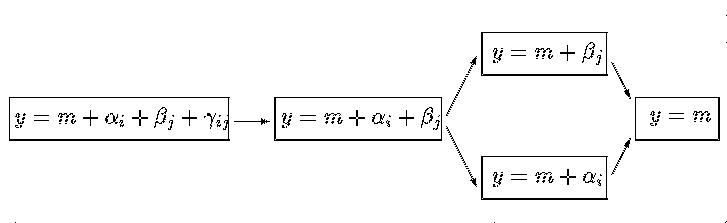
Дисперсионният анализ е част от статистиката, изучаваща влиянието на една или няколко групиращи променливи върху една количествена. Както и в регресията, е прието тази зависима променлива да се нарича отклик. Предикторите, обаче тук се наричат фактори. В основата на дисперсионния анализ лежи възможността сумата от квадрати на отклонения на отклика SSY да бъде разложена на няколко независими суми от квадрати, като по този начин става възможна проверката на различни хипотези за влияние на факторите върху отклика.
В дисперсионния анализ е възприето групиращата променлива да се нарича ''фактор'', стойностите й - ''нива'' на фактора, а отклоненията на средните стойности на групата от общата средна - ''ефекти''. Така с всяко ниво на фактора е свързан един ефект. Ако групите са определени от една групираща променлива, казваме, че се извършва ''еднофакторен'' анализ. Когато факторите са няколко, определянето на групите е по - сложно. Анализът се нарича ''многофакторен''. При двуфакторния анализ, например, се разглеждат, както прости ефекти, свързани с влиянието на всеки фактор поотделно, така и смесени ефекти. Двете групиращи променливи определят толкова групи, колкото е произведението от броя на нивата на двата фактора. Толкова са на брой и смесените ефекти, които отразяват съвместното влияние на факторите върху отклика. Ако се окаже, че такова съвместно влияние отсъствува, т.е. съвместните влияния са малки, следва да се проверяват за значимост простите ефекти.
Основната задача, която се решава с помощта на дисперсионния анализ, може да се формулира най - просто така: да се провери хипотезата дали съвпадат средните стойности на отклика в няколко различни групи от наблюдения. Ако тази хипотеза се отхвърли, необходимо е да се оценят различните средни стойности за всяка група. В този случай се казва, че търсим фиксирани ефекти или разглеждаме модел I.
Друг подход в дисперсионния анализ е оценката на така наречените случайни ефекти или модел II. Приема се, че факторът определя ефекти, които са независими, нормално разпределени, със средни стойности нула и дисперсия, една и съща за всички нива на фактора. Хипотезите, които се проверяват при използуване на такъв модел се отнасят до стойността на тази дисперсия. Въпреки че хипотезите за двата модела са различни, статистиките, с които те се проверяват понякога съвпадат - например, при един фактор. При повече фактори нещата се усложняват неимоверно. Ограниченото място не позволява подробното им излагане. При желание читателят може да се запознае подробно с тях в [Шеффе (1963)] и по - популярно в [Афифи (1982)].
Прието е резултатите от дисперсионния анализ да се представят в така наречените таблици на дисперсионния анализ. В тези таблици за всеки прост или смесен ефект се представя съответната сума от квадрати на отклоненията заедно със степените си на свобода. Така, сравнявайки в определен ред нормираните суми от квадрати с критерия на Фишер, може да се получи представа за влиянието на ефектите.
Най-голяма популярност дисперсионният анализ е придобил в областта на селскостопанския експеримент. С негова помощ се изучава влиянието на различни видове торове и почви върху добива при различни природни условия и под въздействието на редица ненаблюдаеми фактори. Това приложение на дисперсионния анализ в област, където отделно взетия експеримент е скъп и продължителен, още при самото му възникване е поставило пред математиците задачата за оптимизиране на броя на провежданите експерименти. Една голяма част от литературата по дисперсионен анализ е посветена на планирането. В решаването на този проблем са привлечени много математически резултати от други области на математиката, а за експериментаторите се публикуват сборници от планове удовлетворяващи щирок кръг изисквания, произвеждат се програмни системи генериращи такива планове и т.н.
В много случаи прилагането на дисперсионния анализ е еквивалентно на прилагането на регресионния (например, когато всички групиращи променливи - фактори притежават само по две нива), но даже и в този случай поради вложените в себе си възможности да изучава съвместното влияние на факторите той с лекота отговаря на въпроса, кои фактори и в каква комбинация влияят на отклика.
Често се използуват думите дисперсионен анализ и за редица тестове, провеждани като част от други статистически процедури (вж.например, проверка на адекватност на регресионен модел) и то с пълно основание.
Математическата литература по дисперсионен анализ е почти необозрима. Това се дължи главно на факта, че в основата му лежи планирането на многофакторни експерименти, тяхното оптимизиране за задачите поставени от експериментатора. Тук ние ще приведем само елементарните формули за еднофакторен експеримент. Анализът на двуфакторен експеримент, даже и с равен брой наблюдения в клетка, се разклонява в зависимост от типа на ефектите - фиксирани и случайни, прости и смесени и т.н. Класическата книга [Шеффе (1963)] би представлявала полезно пособие за едно сериозно навлизане в тази област.
Моделът на еднофакторния дисперсионен анализ с фиксирани ефекти се записва като регресионен модел по следния начин:
| ||||||||||||||
Тук с ai сме означили ефектите - влиянията съответствуващи на нивата на фактора, а грешките с e - независими случайни величини с разпределение N(0,s2). Индексите i описват възможните нива на фактора, а j - наблюденията в рамките на едно фиксирано ниво. Ясно е, че ако се опитаме да поставим като предиктори изкуствени вектори състоящи се от нули и единици, тази задача би съвпаднала напълно със задачата на регресионния анализ. Съществува обаче проблем в нейното решаване, тъй като рангът на получената матрица е по - малък от необходимия. Затова се налагат (повече или по - малко естествени) ограничения върху оценяваните параметри. В случая това е ограничението
| (11.2) |
Сега вече сме в състояние да извършим оценяване на параметрите на този модел по метода на най - малките квадрати и, (при положение, че имаме достатъчно наблюдения за всяко ниво на фактора) да проверим, например, хипотезата H0:a = 0.
Съответното разлагане на SSy в този случай изглежда така
| (11.3) |
Тук SSr е остатъчната сума от квадрати, а SSm отговаря за влиянието на фактора върху отклика. При изпълнена хипотеза H0:a = 0 двете събираеми са пропорционални на хи-квадрат със степени на свобода съответно N-M и M-1 (с M сме означили броя на непразните нива на фактора, а с N - общия брой наблюдения). F статистиката строим по естествената формула
| (11.4) |
Естествено и тук могат да бъдат избрани по-сложни алтернативи от тривиалната - пълен модел. Такава може да бъде например хипотезата: H1: a1 = - a2. При такава проверка ролите на SSm и SSr се заемат от други суми от квадрати. Такива помощни алтернативи се наричат контрасти.
В много случаи ни е необходимо да направим едновременно заключение за много от параметрите наведнаж. Можем да използуваме следното знаменито неравенство на Бонферони:
| (11.5) |
| (11.6) |
| (11.7) |
Ще започнем решението на задача 1 със следната постановка. Нека броят на нивата на фактора е фиксиран M и броят на наблюдения за всяко ниво - еднакъв k. Търси се константа C такава, че да е изпълнено следното равенство:
| (11.8) |
| ||||||||||||||||||
|
Втората задача решаваме аналогично:
| ||||||||||||
| (11.9) |
Двете разпределения, които се използуват в метода на Тюки са табулирани и могат да се намерят, например в [Hartley(1966)].
|
|
Нека разгледаме един контраст c = {c1,c2,...,cM}ў за параметрите a. Да напомним, че еci = 0 и означим y = cўa = cўb. Тогава
|
Оценките на bi в разглеждания модел са независими и независими в съвкупност от s. Поради линейното условие върху a имаме
|
е Хи-квадрат с M-1 степени на свобода. Следователно
|
| (11.10) |
Тук вече можем да избираме измежду няколко възможни модела:
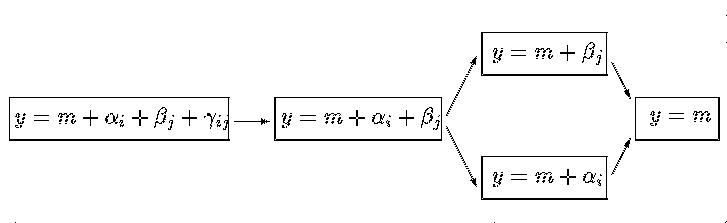
Стрелките показват естествените връзки между моделите, а също и пътя, по който строим и сравняваме нашите хипотези. Прието е, както при полиномната регресия, да започваме от най - сложния модел. Нека разгледаме за пример два такива модела свързани със стрелка:
| |||||
Тук ще разгледаме няколко примера с реални данни заимствани от книгата [Dunn, Clark(1974)].
Пример 1 Пример за еднофакторен дисперсионен анализ.
Целта е да се изучи влиянието на четири типа тор върху добива. За целта 24 еднакви по форма и площ полета са засети с една и съща култура. В дисперсионния анализ се казва, че факторът тор има 4 нива. По случаен начин експериментаторът избрал типът торене върху всяко от полетата, така всеки тип торене се среща 6 пъти. Тези данни трябва да бъдат въведени като две променливи - първата количествена - ДОБИВ и втората - групираща ТОР. Матрицата от данни трябва да изглежда така:
| ДОБИВ | ТОР | ДОБИВ | ТОР | ДОБИВ | ТОР | ДОБИВ | ТОР |
| 99 | 1 | 96 | 2 | 63 | 3 | 79 | 4 |
| 40 | 1 | 84 | 2 | 57 | 3 | 92 | 4 |
| 61 | 1 | 82 | 2 | 81 | 3 | 91 | 4 |
| 72 | 1 | 104 | 2 | 59 | 3 | 87 | 4 |
| 76 | 1 | 99 | 2 | 64 | 3 | 78 | 4 |
| 84 | 1 | 570 | 2 | 396 | 3 | 498 | 4 |
Така въведени данните могат вече да бъдат подложени на дисперсионен анализ. Получаваме следната таблица на дисперсионен анализ:
| Anova 1 Table | |||
| SOURSE OF | SUM OF | D.F. | MEAN |
| VARIATION | SQUARES | SQUARE | |
| TREATMENT | 2940 | 3 | 980 |
| RESIDUAL | 3272 | 20 | 163.6 |
| TOTAL | 6212 | 23 | |
| COMPUTED | |||
| F= 5.99022 | P= .995613 | ||
Стойността на F статистиката, както и вероятността Р са твърде големи и позволяват с висока степен на доверие да отхвърлим хипотезата, че факторът торене не влияе на добива.
Пример 2 Двуфакторен дисперсионен анализ
Ще разгледаме още един пример от [Dunn, Clark(1974)]. В него се изучава добива на ръж като функция от типа на семената и торенето. В този случай торенето се избира по три възможни начина: ниско, средно и високо, и се използуват два типа семена. Експериментаторът и в този случай е разполагал с 24 полета и за всяка от шестте възможни комбинации тор - семе е избрал случайно по 4 полета. Естествено е да разглеждаме фиксирани ефекти.
| ТИП НА | НИВО НА ТОРЕНЕ | ||
| СЕМЕНАТА | НИСКО | СРЕДНО | ВИСОКО |
| 1 | 14.3 | 18.1 | 17.6 |
| 14.5 | 17.6 | 18.2 | |
| 11.5 | 17.1 | 18.9 | |
| 13.6 | 17.6 | 18.2 | |
| 2 | 12.6 | 16.5 | 15.7 |
| 11.2 | 12.8 | 17.6 | |
| 11 | 8.3 | 16.7 | |
| 12.1 | 9.1 | 16.6 | |
Тези данни трябва да се представят в следната форма. Като променливи се определят: откликът ДОБИВ, и фактори (или групиращи променливи) СЕМЕ и ТОР, като последните съответно се кодират. Началото на получената матрица данни ще изглежда така:
| ДОБИВ | СЕМЕ | ТОР | ДОБИВ | СЕМЕ | ТОР |
| 14.3 | 1 | 1 | |||
| 18.1 | 1 | 2 | |||
| 17.6 | 1 | 3 |
Получаваме следната дисперсионна таблица:
| Anova 2 Table | |||
| SOURSE OF | SUM OF | D.F. | MEAN |
| VARIATION | SQUARES | SQUARE | |
| A | 77.4004 | 1 | 77.4004 |
| B | 99.8725 | 2 | 49.9362 |
| AB | 44.1058 | 2 | 22.0529 |
| RESIDUAL | 21.9975 | 18 | 1.22208 |
| TOTAL | 243.376 | 23 | |
| Fixed | |||
| FA | FB | FAB | |
| 63.3348 | 40.8615 | 18.0453 | |
| .999999 | .999999 | .999949 | |
| Random | |||
| FA | FB | ||
| 3.50975 | 2.26438 | ||
| .798127 | .693663 | ||
От тази таблица заключаваме, че съществува изразено взаимодeйствие между торенето и типа на семената при влиянието им върху добива -FAB = 18.0453, а вероятността .999949 говори, че хипотезата за незначимост на смесените ефекти се отхвърля. След като смесените ефекти на двата фактора са значими, не бива да проверяваме поотделно хипотезите за простите ефекти. Може веднага да се приеме, че влиянието на типа на семената и торенето като цяло върху добива е съществено.
Тъй като този пример не е особено поучителен, не илюстрира пълните възможности на процедурата, ще разгледаме още един пример от областта на психологията.
Пример 3 Данните за скоростта на реакцията на човек при подаване на светлинен (A,C) и звуков (B,D) сигнали.
Изучават се два типа реакция: при A и B - реакцията е проста, а при C и D - с избор. Естествено е, да разглеждаме две групиращи променливи. Първата описва типа на сигнала (светлинен или звуков), а втората - условията на експеримента (с или без избор). За да въведем данните в паметта, трябва да ги прекодираме аналогично на предния пример. За тези данни таблицата на двуфакторния анализ изглежда иначе:
| Anova 2 Table | |||
| SOURSE OF | SUM OF | D.F. | MEAN |
| VARIATION | SQUARES | SQUARE | |
| A | 123932. | 1 | 123932. |
| B | 5206.24 | 1 | 5206.24 |
| AB | 62.1323 | 1 | 62.1323 |
| RESIDUAL | 24495.7 | 64 | 382.746 |
| TOTAL | 153696. | 67 | |
| Fixed | |||
| FA | FB | FAB | |
| 323.797 | 13.6023 | .162332 | |
| 1 | .999531 | .311639 | |
| Random | |||
| FA | FB | ||
| 1994.65 | 83.7929 | ||
| .985748 | .930728 | ||
Тук вече взаимодействието между факторите отсъствува - статистиката FAB е незначима. По-отделно обаче, влиянието и на двата фактора е значимо и не може да бъде пренебрегнато. При желание може да се пресметнат оценените вътрешно групови средни стойности при адитивното влияние на двата фактора.
Нека разгледаме сега пак регресионния модел със свободен член. Ше включим в модела групираща променлива и нека тя да е една. Ще представим наблюденията върху нея в матрицата Z. Сега моделът приема следната форма:
| (11.11) |
Групиращата променлива приема стойности от 1 до G. Матрицата Z е с размерност (n xG), като всеки ред е индикатор (съдържа нули и една единица) за групата, на която принадлежи съответното наблюдение. Сега броят на параметрите е вече m + G и разбира се, трябва да бъде изпълнено неравенството m + G < N. С m сме означили вектора от параметри (с размерност G), отразяващ влиянието на стойността на групиращата променлива за дадено наблюдение. Този модел е обект на така наречения ковариационен анализ (вж. [Шеффе (1963)]), където се предполага зависимост и на вектора a от стойността на групиращата променлива.
При G = 1 моделът се свежда към класическа линейна регресия със свободен член. При G > 1 формулите за пресмятане претърпяват незначителни изменения. При a = 0 параметрите m очевидно са ''вътрешно-груповите'' средни стойности с естествени си оценки. За да се запази това им качество и при ненулево a, във всички формули по горе матрицата XўX/n трябва да се замести с вътрешно-груповата ковариационна матрица Vi и числото n да се замести с n-G.