Тук ще представим една процедура от многомерния анализ на данни базирана на вероятностен модел. Другото название на процедури от този тип е разпознаване на образи.
Тази статистическа процедура се използува, когато се нуждаем от "прогнозиране" стойностите на групираща променлива. Понякога това се нарича класификация или разпознаване на образи. Нека нашата извадка е нееднородна или с други думи, се състои от няколко групи наблюдения с различни вероятностни характеристики. Целта ни е да се научим от тази извадка, по зададени параметри на дадено наблюдение, да определим принадлежността му към класа, от който произлиза.
В първата си част, фазата на обучение, процедурата на дискриминантния анализ обработва тази информация с цел да я кондензира в тъй наречените решаващи правила. Когато те са получени, естествено е те да бъдат изпробвани върху обектите от обучаващата извадка или върху други обекти с известен клас. При положение, че тези обекти (или поне достатъчно голям процент от тях) бъдат класифицирани правилно, можем да очакваме, че разпознаващите правила са добри и коректно ще работят и за обекти от неизвестен клас.
Разбира се, конкретното прилагане на различните методики на дискриминантния анализ има ред тънкости. Тук ще се спрем по - подробно на най - разпространената процедура за стъпков линеен дискриминантен анализ. Тя притежава ред недостатъци, но и някои преимущества - в частност дава прости решаващи правила.
В линейния дискриминантен анализ се строят линейни дискриминантни функции от предикторите. За всеки клас има точно една такава функция. Правилото за класификация изглежда така:
Наблюдението се класифицира към класа с максимална дискриминантна функция.

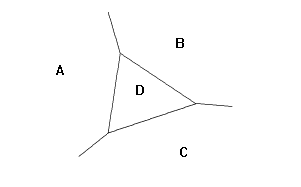
Областта от стойности на предикторите, при попадане в която наблюденията се класифицират към даден клас, е изпъкнал многоъгълник (възможно отворен). Тя се нарича класификационно множество на класа. При два предиктора и 4 класа класификационните множества биха могли да изглеждат по указания начин. На фигура 12.1 с големи букви са отбелязани груповите средни.
Когато класовете са ясно разграничени, не е трудно те да бъдат отделени. Когато обаче те се пресичат, въпросът за оптимален (с най - малко грешки) избор на класификационни правила е сложен и изисква допълнителна априорна информация.
Линейният дискриминантен анализ предполага, че разпределенията на количествените променливи (предикторите) вътре в класовете са нормални и се различават само по средните си стойности. Тогава процедурата произвежда оптимални решаващи правила. Разбира се, тя може да се използува и при случайна (по групиращата променлива) извадка, но появата на празен клас е недопустима.
Когато броят на количествените променливи е по - голям, за простотата на решаващите правила е съществено да се отберат за предиктори само тези променливи, които носят важната за разделянето информация. В това помага статистиката на Махалонобис. Тя позволява да се провери хипотезата за съвпадане на груповите средни на предикторите като цяло. За простота и тук, вместо критичната област за статистиката, се използува вероятността съответно разпределената случайна величина да не надхвърли стойността на статистиката. Тази вероятност расте докато променливите допринасят за по - доброто разделяне на класовете и започва да намалява, когато предикторите станат твърде много. Естествено, добро разделяне може да се очаква, само когато хипотезата се отхвърля с висока вероятност.
Нека вече са избрани най - добрите променливи за предиктори. Това още не означава, че са построени класификационните множества. Да напомним, че основна цел на дискриминантния анализ е да се получи правило за причисляване на едно ново наблюдение към даден клас. За това наблюдение може да съществува априорна информация за неговата възможна принадлежност към класовете. Прието е такава информация да бъде формулирана в термини на априорни вероятности, които са необходими за определяне на оптимални класификационни правила.
Ако такава информация не съществува, естествено е априорните вероятности на класовете да се приемат за равни. Когато пък извадката е случайна и новото наблюдение се избира по същия начин, може те да се приемат за пропорционални на обема на класовете в обучаващата извадка.
Изборът на априорните вероятности фиксира оптимални дискриминантни функции и класификационни правила. Не е удобно обаче, за всяко ново наблюдение да се въвеждат априорни вероятности. Това е свързано и със значителни изчислителни трудности, особено когато броят на класовете е голям. Един възможен начин за заобикаляне на това неудобство е представянето на класовете с помощта на няколко групиращи променливи. Такова представяне съответствува и на редица практически задачи. Ако са известни стойностите на поне една от групиращите променливи, това е съществена априорна информация - фиксирането на тази променлива е еквивалентно на задаването на нулева априорна вероятност за поне половината от класовете.
| (12.1) |
Тук f е плътността на нормалното разпределение със средна стойност m(g) и ковариационна матрица C, а c е нормираща константа (такава, че еq(g) = 1).
| (12.2) |
Класификационните правила могат да бъдат записани във вида:
| (12.3) |
за които след логаритмуване и съкращаване, получаваме:
| (12.4) |
Векторът b(g) и числото a(g) се получават по формулите:
| (12.5) |
Когато групиращите променливи са повече от една, броят на класовете G нараства. Вероятността за поява на празни клетки (n(g) = 0) при случайна извадка с ограничен обем рязко се увеличава. Затруднява се и оценката за {m(g)}. В такива случаи се препоръчва използуването на оценки, получени от линеен модел, като се направят съответните проверки с методите на дисперсионния анализ. Съответно, ще се промени и оценката за C. Аналогично, за оценяване на честотите n(g) могат да се прилагат тъй наречените логаритмично - линейни (log - linear) модели.
Аналогично на стъпковия регресионен анализ и тук е възприета
концепцията за избор на подходящ набор от количествени
променливи, с които да построим модела. Единственото средство,
което ни трябва са аналозите на P(F-to-enter) и
P(F-to-remove). Те се строят аналогично на регресията,
но ролята на сумите от квадрати играят
- вътрешно - груповата ковариационна матрица
- между - групова ковариационна матрица.
Както и в едномерния случай, така и в многомерния е верно следното равенство:
| |||||||||||||||||||||||||||||||||||||
Матрицата SSim се тълкува като ''сума от квадрати'', отговаряща на разсейването на данните около техните локални средни и с нейна помощ се строи оценка за вътрешно - груповата ковариационна матрица C:
|
Матрицата SSin се тълкува като ''сума от квадрати'', отговаряща на разсейването на груповите средни и с нейна помощ се строи оценка за между - груповата ковариационна матрица Cmg:
|
Точно изменението на детерминантата на тази матрица ни служи за критерий при избора на нова променлива за въвеждане в модела или за нейното отстраняване.