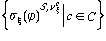 =min
=min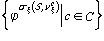 ,
,| Previous | Next | Contents |
Теорема за стойността на резултата от прилагане на субституция към формула. Нека j е произволна формула. Тогава за всяка субституция s, приложима към j, и всяка конфигурация (S,v) е в сила равенството s(j)S,v=js(S,v).
Доказателство. Случаят, когато формулата j е атомарна, се съдържа в споменатата вече доказана теорема. Сега ще покажем, че свойството, за което става дума в теоремата, се запазва при образуване на отрицание, на конюнкция и на дизюнкция, а също при поставяне на квантори. Нека j е формула, притежаваща доказваното свойство. За да докажем, че и формулата Шj го притежава, разглеждаме произволна субституция s, приложима към Шj, и произволна конфигурация (S,v) и правим следните пресмятания:
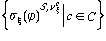 =min
=min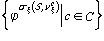 ,
,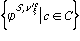 .
.
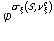 =
=
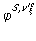 .
. )=(S,w),
)=(S,w),
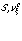 .
.
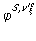 .
.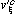 съвпадат върху множеството
на свободните променливи на формулата j. Нека h е коя да е от тези променливи.
Ако h е променливата x, то равенството
съвпадат върху множеството
на свободните променливи на формулата j. Нека h е коя да е от тези променливи.
Ако h е променливата x, то равенството
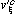 (h)
(h)
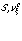 ,
, 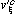 (h)=s(h)S,v
(h)=s(h)S,v и v съвпадат върху множеството
на свободните променливи на терма s(h). Тези две оценки наистина съвпадат върху
въпросното множество, защото те могат да имат различни стойности само
за променливата x, а тя не е свободна променлива на s(h) благодарение на това,
че субституцията s не привнася x във формулата j. С това доказателството на
теоремата е завършено.
и v съвпадат върху множеството
на свободните променливи на терма s(h). Тези две оценки наистина съвпадат върху
въпросното множество, защото те могат да имат различни стойности само
за променливата x, а тя не е свободна променлива на s(h) благодарение на това,
че субституцията s не привнася x във формулата j. С това доказателството на
теоремата е завършено.Доказаната теорема ще ни позволи да пренесем за произволни формули и други неща, които по-рано изказахме само за безкванторни формули.
Лема за запазване на тъждествената вярност при прилагане на субституция към произволна формула. Ако j е формула, която е тъждествено вярна в дадена структура S, а s е субституция, приложима към j. Тогава формулата s(j) също е тъждествено вярна в S.
Доказателството на тази лема е напълно аналогично на доказателството на аналогичната лема, отнасяща се до прилагане на субституция към безкванторна формула.
Както и в по-рано разглеждания случай, всеки резултат от прилагане на субституция към дадена формула ще наричаме частен случай на тази формула. Току-що доказаната лема може да се изкаже така: всички частни случаи на формула, тъждествено вярна в дадена структура, са също тъждествено верни в тази структура. Оттук разбира се се вижда, че всички затворени частни случаи на формула, тъждествено вярна в дадена структура, са верни в тази структура. Обратното в общия случай не е вярно, но за да е налице то, имаме същото достатъчно условие както по-рано.
Достатъчно условие за тъждествена вярност при вярност на затворените частни случаи. Нека S=(C,I) е такава структура, че всеки елемент на C е стойност в S на някой затворен терм, нека j е формула и нека всички затворени частни случаи на j са верни в S. Тогава j е тъждествено вярна в S.
Единственият допълнителен момент в доказателството на това твърдение в сравнение с аналогичното по-раншно доказателство е това, че трябва да се уверим в приложимостта на разглежданата в него субституция към формулите, към които искаме да я прилагаме. Това обаче е ясно от обстоятелството, че въпросната субституция преобразува всяка променлива в затворен терм, а такива субституции са приложими към всяка формула.
От лемата за запазване на тъждествената вярност при прилагане на субституция към произволна формула лесно се получава следното твърдение.
Лема за запазване на следването при прилагане на субституция. Нека j и y
са формули, за които е изпълнено съотношението j y, а s е субституция, която е
приложима както към j, така и към y. Тогава е в сила и съотношението
s(j)
y, а s е субституция, която е
приложима както към j, така и към y. Тогава е в сила и съотношението
s(j) s(y).
s(y).
Доказателство. При направените предположения може да се твърди, че импликацията j®y е тъждествено вярна. От друга страна приложимостта на s към формулите j и y гарантира нейната приложимост и към споменатата импликация, а също равенството s(j®y)=s(j)®s(y). Това показва, че и импликацията s(j)®s(y) е тъждествено вярна.
Следствие. Ако j и y са еквивалентни формули, а s е субституция, която е приложима както към j, така и към y, то формулите s(j) и s(y) също са еквивалентни.
С помощта на лемата за запазване на следването при прилагане на субституция ще докажем следната теорема.
Теорема за семантичната връзка между генерализация, частен случай и екзистенциализация. Нека j е формула, x1, ..., xn са различни променливи, а t1, ..., tn са такива термове, че субституцията (x1,...,xn:=t1,...,tn) е приложима към j. Тогава са изпълнени съотношенията
 (x1,...,xn:=t1,...,tn)(j)
(x1,...,xn:=t1,...,tn)(j) $x1...$xnj.
$x1...$xnj.Доказателство. Да означим със s споменатата в теоремата субституция. Очевидно s съвпада със субституцията (:=) върху множеството на свободните променливи на всяка от формулите "x1..."xnj и $x1...$xnj. Следователно s е приложима към всяка от тези две формули и са изпълнени равенствата
 j
j $x1...$xnj.
$x1...$xnj. q
q $xq
$xq "x2..."xn-1"xnj
"x2..."xn-1"xnj ...
...  "xn-1"xnj
"xn-1"xnj "xnj
"xnj j,
j, $xnj
$xnj $xn-1$xnj
$xn-1$xnj ...
...
 $x2...$xn-1$xnj
$x2...$xn-1$xnj $x1$x2...$xn-1$xnj.
$x1$x2...$xn-1$xnj.
Накрая ще се спрем на въпроса за това как в известен смисъл може да бъде
преодоляна неприложимостта на дадена субституция към дадена формула. Да предположим,
че j е формула, a s е субституция, която не е приложима към j. Бихме
могли да използваме задоволителен от семантична гледна точка заместител на
прилагането на s към j, като се основаваме на следните две обстоятелства:
1. Може да се намери формула jў, еквивалентна на j и имаща същите свободни
променливи, такава, че s да бъде приложима към jў.
2. Винаги, когато jў е формула, еквивалентна на j, субституцията s е
приложима към jў и (S,v) е конфигурация, в сила е равенството s(jў)S,v=js(S,v).
За да се убедим във верността на първото от горните твърдения, нека означим с X0 множеството на променливите, които s не привнася във j. По теоремата за ограничаване на избора на свързаните променливи може да се намери такава формула jў, еквивалентна на j, че да бъдат изпълнени условията СВО(jў)=СВО(j), СВЪ(jў)НX0. Първото от тези условия гарантира, че s привнася във jў точно онези променливи, които привнася във j. Оттук веднага следва приложимостта на s към jў, като се вземе пред вид второто от условията и се приложи твърдение 1 от предходния въпрос.
Второто от изказаните две твърдения се проверява, като се забележи, че изказаните в него предположения за j, jў, s, S, v осигуряват равенствата s(jў)S,v=jўs(S,v)=js(S,v).
Пример 1. Нека j е формулата p(y)«$xq(x,y), където p и q са съответно едноместен и двуместен предикатен символ, а x и y са различни променливи. Нека s е субституцията (y:=x). Тази субституция не е приложима към формулата $xq(x,y) и следователно не е приложима и към j. Ако означим обаче с jў формулата p(y)«$zq(z,y), където z е някаква променлива, различна и от x, и от y, то j е еквивалентна на jў и s е приложима към jў. Като приложим s към jў, получаваме формулата p(x)«$zq(z,x), която от семантична гледна точка би могла да играе ролята на несъществуващия по нашите дефиниции резултат от прилагането на s към j, тъй като стойността й в произволна конфигурация (S,v) ще бъде равна на js(S,v).
Забележка. До резултата от горния пример бихме могли да стигнем по друг начин, като забележим, че формулата p(x)«$zq(z,x) може да се получи от j чрез преименуването (x,y,z:=z,x,y)#, и приложим теоремата за стойността на резултата от преименуване (за да получим същото заключение както по-горе за стойността на тази формула в произволна конфигурация (S,v), би трябвало още да отчетем, че оценката, която е втора компонента на s(S,v), съвпада с оценката v(x,y,z:=z,x,y) за единствената свободна променлива y на j). Подобен подход обаче не би бил възможен, ако модифицираме горния пример така, както е посочено в следващия.
Пример 2. Нека j е същата формула както в пример 1, но s е субституцията (y:=f(x)), където f е едноместен функционален символ. Тогава s отново не е приложима към j, а е приложима към jў. Резултатът от прилагането й е формулата p(f(x))«$zq(z,f(x)), а тя не може да се получи от j чрез преименуване на променливите. За стоиността й в произволна конфигурация (S,v) отново можем да твърдим, че е равна на js(S,v).
Последно изменение: 26.07.1999 г.
| Previous | Next | Contents |