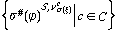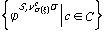Previous  Next  Contents

 

ПРЕИМЕНУВАНЕ НА ПРОМЕНЛИВИ

    Досега сме дефинирали какво значи резултат от прилагане на една субституция към безкванторна формула. Твърде желателно е това понятие да се разшири така, че субституциите да могат да се прилагат към произволни формули. За разлика от това, което имаме в случая на безкванторните формули, при формулите, съдържащи квантори, в общия случай не би било разумно при прилагане на субституция всички участия на променливи да се заменят със съответните им термове. Една очевидна причина за това е обстоятелството, че една такава замяна би могла да породи дума, която изобщо не е формула. Например ако във формулата "xp(x), т.е. в думата [x]p(x), където x е променлива, а p е едноместен предикатен символ, ние заменим променливата x на двете места, където тя е използвана при построяването на формулата, с някакъв терм t, различен от променлива, получената дума [t]p(t) не ще бъде формула. Тази причина разбира се не е налице за такива субституции, които заместват променливи само с променливи, но даже и в този случай са възможни проблеми, които ще илюстрираме с един пример. Тъй като споменатите проблеми възникват не само в математическата логика, но и при излагането на математиката на обичайния не напълно формализиран език, въпросния пример ще предпочетем да изложим без да прибягваме към езика на математическата логика. Ще покажем как небрежното заменяне на една променлива с друга може да ни доведе до привидно доказателство на явно невярно твърдение.

    Пример 1. Да се условим с буквите x и y да означаваме естествени числа. Тогава дефиницията кога едно естествено число y е четно би могла да се изкаже така:

y е четно точно тогава, когато съществува такова x, че y=2x.
За да установим например, че числото 5 не е четно, можем в горната дефиниционна равносилност да заместим променливата y с 5; тогава ще получим равносилността
5 е четно точно тогава, когато съществува такова x, че 5=2x,
след което можем да използваме несъществуването на x със свойството 5=2x. Аналогично, за да установим, че при произволен избор на y съответното число 6y е четно, можем да заместим y с 6y; ще получим равносилността
6y е четно точно тогава, когато съществува такова x, че 6y=2x,
а след това можем да използваме съществуването на x със свойството 6y=2x (такова x е числото 3y). Действайки привидно аналогично, да си мислим, че е дадено произволно x и да заместим в дефиниционната равносилност, с която работим, буквата y с x, като просто пишем x там, където виждаме y. Получаваме равносилността
x е четно точно тогава, когато съществува такова x, че x=2x.
Очевидно твърдението "съществува такова x, че x=2x" е вярно, защото 0=2.0. Но тогава по написаната равносилност твърдението "x е четно" също трябва да бъде вярно, т.е. получихме, че произволно избрано естествено число е четно. Получаването на този абсурден резултат стана възможно поради това, че при заместването на y с x възникна едно ново участие на буквата x в равенството след думата "че", в което участие тя по смисъл би трябвало да означава произволно избраното естествено число, с което се занимаваме, за разлика от наличната отпреди буква x, но формално това различие не личи от записа на получената чрез заместването равносилност. Използвайки логическа терминология, можем да кажем, че първоначалното x в равенството е свързано, докато новопоявилото се би трябвало да е свободно, а погледнато формално, то също се оказва свързано. Ако искаме да демонстрираме същите неща с формули на предикатното смятане, бихме могли да пишем например p(y) вместо "y е четно", q(x,y) вместо "y=2x" и еквиваленцията p(y)«$xq(x,y) вместо дефиницията за четно число, а след това, опитвайки се към тази еквиваленция да приложим субституцията (y:=x), да получим еквиваленцията p(x)«$xq(x,x).

    Неприятността, с която току-що се срещнахме, е пример за тъй наречената колизия на променливите. Как да я избягваме в общия случай, ще видим по-нататък, а засега ще разгледаме един специален вид субституции, които, ако ги прилагаме по невъзможния в общия случай най-непосредствен начин, не водят до такава неприятност.

    Да се условим да наричаме преименуваща субституция такава субституция, която преобразува всяка променлива пак в променлива и освен това е обратима, т.е. преобразува всеки две различни променливи пак в различни.

    Пример 2. Ако x, y, z са различни помежду си променливи, то субституцията (y:=x) не е преименуваща, защото преобразува x и y в една и съща променлива (а именно в y), докато субституциите (:=), (x,y:=y,x) и (x,y,z:=y,z,x) са преименуващи. Ако x0,x1,x2,... е една безкрайна редица от различни помежду си променливи, то преименуваща е и субституцията, която при i=0,1,2,... преобразува xi в x2i, а всички променливи, които не са членове на споменатата редица (в случай че има такива променливи), преобразува в самите тях.

    Пример 3. Всяко обратимо изображение на крайно множество от променливи в множеството на всички променливи може да бъде продължено до финитарна преименуваща субституция. И наистина, нека r е такова изображение. Да положим D=dom(r), R=range(r). Тогава D и R  са крайни множества с равен брой елементи. Поради равенствата D\R=D\(DЗR), R\D=R\(DЗR), крайните множества D\R и R\D също се оказват с равен брой елементи и значи може да се намери обратимо изображение rў на R\D върху D\R. Да разгледаме сега субституцията s, дефинирана по следния начин:

s(h) = { r(h) при hОD,
rў(h) при hОR\D
и s(h)=h във всички останали случаи. Очевидно s е финитарна и е продължение на даденото изображение r, а лесно се проверява, че s е обратима.

    Забележка. Когато една преименуваща субституция е финитарна, множеството на нейните стойности съвпада с множеството на всички променливи (доказателството може да се извърши, като се използва, че всяка преименуваща субституция s преобразува елементите на съответното множество {xОX|s(x)№x} пак  в елементи на това множество).

    Да предположим, че е дадена една преименуваща субституция s. Ще дефинираме какво значи една формула да е s-вариант на дадена формула. Дефиницията е индуктивна и се състои от следните точки:
          В1. Ако a е атомарна формула, то s(a) е s-вариант на a.
          В2. Ако jў е s-вариант на j, то Шjў е s-вариант на Шj.
          В3,4. Ако jў е s-вариант на j и yў е s-вариант на y, то jў&yў е s-вариант на j&y и jўЪyў е s-вариант на jЪy.
          В5,6. Ако jў е s-вариант на j, а x е променлива, то "s(x)jў е s-вариант на "xj и $s(x)jў е s-вариант на $xj.

    Пример 4. Нека x, y, z, t са различни помежду си променливи и нека j е формулата "x$yШp(x,y,z), където p е триместен предикатен символ. Тогава формулите "x$tШp(x,t,z), "y$xШp(y,x,z) и "y$zШp(y,z,x) са s-варианти на j съответно при s=(y,t:=t,y), s=(x,y:=y,x) и s=(x,y,z:=y,z,x).

    Да продължим да предполагаме, че е дадена една преименуваща субститъуция s. С индукция относно построението на формулите на предикатното смятане лесно се доказва, че всяка формула притежава точно един s-вариант. Ако на коя да е формула съпоставим нейния единствен s-вариант, получаваме едно изображение на множеството на формулите в себе си, което ще наричаме преименуване, съответно на s, и ще означаваме с s#. От дадените дефиниции става ясно, че за всяка атомарна формула a е в сила равенството s#(a)=s(a) и за произволни формули j, y и произволна променлива x са изпълнени равенствата

s#(Шj)=Шs#(j),  s#(j&y)=s#(j)&s#(y),  s#(jЪy)=s#(j)Ъs#(y),
s#("xj)="s(x)s#(j),  s#($xj)=$s(x)s#(j).

    С индукция относно построението на безкванторните формули се показва, че за всяка безкванторна формула j имаме равенството s#(j)=s(j), а чрез индукция относно построението на формулите на предикатното смятане - това, че за всяка формула j на предикатното смятане са в сила равенствата

СВО(s#(j))={s(h)|hОСВО(j)},  СВЪ(s#(j))={s(h)|hОСВЪ(j)}.
Добре е да отбележим, че при индуктивните стъпки, отговарящи на използването на квантор, доказателството на първото от тези равенства използва обратимостта на s. Това е така, понеже на споменатото място от доказателството става нужда да се използва, че за всяка формула j и всяка променлива x е в сила равенството
{s(h)|hОСВО(j)}\{s(x)}={s(h)|hОСВО(j)\{x}}
(на съответното място от доказателството на другото от равенствата се използва, че за всяка формула j и всяка променлива x имаме равенството
{s(h)|hОСВЪ(j)}И{s(x)}={s(h)|hОСВЪ(j)И{x}},
то обаче е вярно за произволно изображение s с дефиниционна област множеството на променливите).

    Семантичната връзка между j и s#(j) се описва от следното твърдение, в което vs означава композицията на v и s, дефинирана чрез равенството vs(h)=v(s(h)).

    Теорема за стойността на резултата от преименуване. Нека е дадена една структура S. Тогава за всяка формула j на предикатното смятане при произволна оценка v в S на променливите е в сила равенството s#(j)S,v=jS,vs.

    Доказателство. Използваме индукция относно построението на j. Ако j е атомарна, интересуващото ни равенство следва от изпълненото в този случай равенство s#(j)=s(j) като се използват теоремата за стойността на резултата от прилагане на субституция към такава формула и обстоятелството, че имаме равенството s(S,v)=(S,vs). Индуктивните стъпки, отговарящи на използването на отрицание, конюнкция и дизюнкция, са съвсем лесни, затова ще преминем направо към индуктивната стъпка, отговаряща на използването на квантор за общност. И така, нека j е такава формула, че за всяка оценка v в S на променливите да бъде в сила равенството от формулировката на теоремата, и нека x е дадена променлива. Тогава, означавайки с C носителя на S, за произволна оценка v в S на променливите ще имаме 

s#("xj)S,v=("s(x)s#(j))S,v=min=min.
Благодарение на обратимостта на субституцията s обаче имаме равенството 
(очевидно и двете страни на това равенство имат стойност c за променливата x, а ако h е променлива, различна от x, то и променливата s(h) е различна от променливата s(x), тъй че стойността на лявата страна за h е равна на v(s(h)) и значи пак съвпада със стойността на дясната). Следователно 
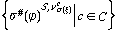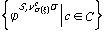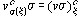
s#("xj)S,v=min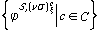=("xj)S,vs,
т.е. равенството от формулировката на теоремата остава в сила и след замяната на j със "xj. Разбира се индуктивната стъпка, която отговаря на използването на квантор за съществуване, е напълно аналогична.

    За нас ще бъде особено полезно едно следствие от горната теорема, което ще изкажем сега.

    Теорема за преименуване на свързани променливи. Нека j е формула, а s е такава преименуваща субституция, че s(h)=h за всяка свободна променлива h на j. Тогава формулата j е еквивалентна на формулата s#(j) и двете формули имат едни и същи свободни променливи.

    Доказателство. Нека S е произволна структура, а v е произволна оценка в S на променливите. Тогава според предходната теорема имаме равенството s#(j)S,v=jS,vs. От друга страна обаче имаме и равенството jS,vs=jS,v, тъй като оценките vs и v съвпадат върху множеството на свободните променливи на j. Следователно s#(j)S,v=jS,v.Следователно s#(j)S,v=jS,v. С това еквивалентността на формулите j и s#(j) е установена. Твърдението, че свободните променливи на тези формули са едни и същи, следва от отбелязаната в общия случай връзка между СВО(j) и СВО(s#(j)) и от обстоятелството, че в случая s преобразува свободните променливи на j в самите тях.

    Следствие. Ако j е затворена формула, то за всяка преименуваща субституция s формулата j е еквивалентна на формулата s#(j) и тя също е затворена.

    Понякога се оказва подходящо теоремата за преименуване на свързани променливи и следствието от нея да се приложат не към цялата формула, с която имаме работа, а към някоя нейна подформула, и това, че замяната на въпросната подформула с еквивалентна на нея ще даде формула, еквивалентна на първоначалната, да се получи като се използват по-рано изучените свойства на еквивалентността на формули.

    Пример 5. Нека q е формулата p(x)&$xШp(x), където p е едноместен предикатен символ, а x е променлива. Променливата x е както свободна, така и свързана променлива на q. За да получим формула, еквивалентна на q, но без тази особеност, можем първо да приложим следствието от теоремата за преименуване на свързани променливи към формулата $xШp(x) и да заключим, че тя е еквивалентна например на формулата $yШp(y), където y е променлива, различна от x. Оттук ще следва, че цялата формула q от своя страна е еквивалентна на формулата p(x)&$yШp(y).

    С помощта на теоремата за преименуване на свързани променливи ще докажем следното полезно твърдение.

    Теорема за ограничаване на избора на свързаните променливи. Нека X0 е дадено безкрайно множество от променливи. Тогава всяка формула е еквивалентна на някоя формула със същите свободни променливи, на която всички свързани променливи принадлежат на X0.

    Доказателство. Ще използваме индукция, съобразена с дефиницията за формула. Тъй като твърдението на теоремата е тривиално вярно за атомарните формули, а индуктивните стъпки, отнасящи се до образуване на отрицание, на конюнкция и на дизюнкция, са съвсем прости, ще разгледаме само индуктивната стъпка, отнасяща се до поставяне на квантор. Ще се ограничим със случая на  квантор за общност. Нека j е формула с доказваното свойство и jў е еквивалентна на нея формула, удовлетворяваща условията СВО(jў)=СВО(j), СВЪ(jў)НX0. Нека x е произволна променлива. Ще трябва да докажем, че и формулата "xj има въпросното свойство. Разбира се тя е еквивалентна на формулата "xjў и двете формули имат едни и същи свободни променливи. Ако x принадлежи на X0, то всичко е наред, тъй като в този случай всички свързани променливи на "xjў ще принадлежат на X0. Ако пък x не принадлежи на X0, то можем да изберем някоя променлива h от X0, която не принадлежи на крайното множество СВО("xjў)ИСВЪ("xjў), и, прилагайки теоремата за преименуване на свързани променливи, да заключим, че формулата "xjў е еквивалентна на формулата (x,h:=h,x)#("xjў) и двете формули имат едни и същи свободни променливи (всички свързани променливи на формулата (x,h:=h,x)#("xjў) принадлежат на X0, защото множеството на свързаните й променливи се получава от множеството на свързаните променливи на "xjў чрез замяна на x с h).

    Като използваме, че за всяка формула j множеството X\СВО(j) е безкрайно, и приложим горната теорема, получаваме:

    Следствие. Всяка формула е еквивалентна на някоя формула със същите свободни променливи, на която никоя от свързаните променливи не е нейна свободна променлива.

 

Последно изменение: 6.10.2000 г.

 Previous  Next  Contents