THE t DISTRIBUTION

DEFINITION

The t distribution is a theoretical probability distribution. It is symmetrical, bell-shaped, and similar to the standard normal curve. It differs from the standard normal curve, however, in that it has an additional parameter, called degrees of freedom, which changes its shape.

DEGREES OF FREEDOM

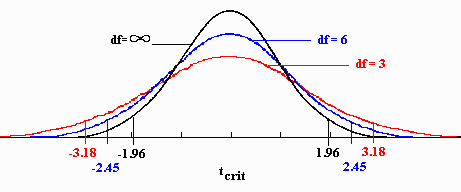
Degrees of freedom, usually symbolized by df, is a parameter of the t distribution which can be any real number greater than zero (0.0). Setting the value of df defines a particular member of the family of t distributions. A member of the family of t distributions with a smaller df has more area in the tails of the the distribution than one with a larger df.

The effect of df on the t distribution is illustrated in the four t distributions below.

Note that the smaller the df, the flatter the shape of the distribution, resulting in greater area in the tails of the distribution.

RELATIONSHIP TO THE NORMAL CURVE

The astute reader will no doubt observe that the t distribution looks similar to the normal curve. As the df increase, the t distribution approaches the standard normal distribution (=0.0, =1.0). The standard normal curve is a special case of the t distribution when df=. For practical purposes, the t distribution approaches the standard normal distribution relatively quickly, such that when df=30 the two are almost identical.