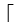Алгоритъм за построяване на пирамида BottomUp

• Псевдокод
• Анализ
• Реализация на Java
• Итеративна реализация

Псевдокод

  Алгоритъм BottomUp
  
  Вход:  Масив V от size на брой елемента
  Изход: Пирамида heap
  
  if (V.size <= 1) return
  
  vLeft  = V[1..sizeL]
  vRight = V[sizeL.. size-1]  
  
  Left  <-- BottomUpHeap(vLeft)
  Right <-- BottomUpHeap(vRight)
  
  heap <-- newHeap(V[0], Left, Right)

Анализ

Алгоритъмът е линеен в най-лошия случай: O(n)

Ако T(n) означава времето за изпълнение на bottomUp, където c е константа, такава че времето за отсяване на корена в пирамида с височина h e не по-голямо от c*(h - 1), тогава:

T(n) <= c * (n - h(n) - 1) <= c * n,

h(n) = 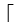log₂(n+1)

  T(n) = c * (h - 1) + T(size(Left)) + T(size(Right)) <=
      <= c * (h - 1) + c * (size(left) - h(left) - 1 + size(right) - h(right) - 1) =
       = c * ( h - 1 + (size(left) + size(right) + 1) - 3 - h(left) - h(right) ) <=
      <= c * ( h - 1 + n - 3 - (h - 1) - (h - 2)) = c * ( n - h - 1).

Реализация на Java за Bottom-Up

  /**
   * Bottom-Up in-place construction.
   * Constructs a heap and fills it with the objects from items
   * using an algorithm for bottom-up construction.
   */
  public ArrayHeap(Comparator comparator, Item[] items) {
    super(comparator);    
    size = items.length;
    height = computeHeight(size);    
    elements = new ArrayList(size);
    for (int i = 0; i < size; i++) { elements.add(items[i]); }
    bottomUp(0);
  }
  
  /**
   * Constructs the items of the subarray starting from sInx, i.e.
   * items[sInx..size - 1] into the heap container.
   */
  public void bottomUp(int sInx) {
    if (sInx + 1 >= elements.size()) 
      return;
    bottomUp(getLeft(sInx));
    bottomUp(getRight(sInx));
    downBubbling(sInx);
  }

Итеративна реализация на Bottom-Up на място

    void bottomUpHeap(Item[] items) {
        for (int i = items.length / 2 - 1; i >= 0; i--) {
            downBubbling(items, i);
        }
    }